No CrossRef data available.
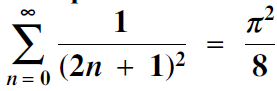 $\sum\limits_{n = 0}^\infty {{1 \over {{{(2n + 1)}^2}}} = {{{\pi ^2}} \over 8}} $
$\sum\limits_{n = 0}^\infty {{1 \over {{{(2n + 1)}^2}}} = {{{\pi ^2}} \over 8}} $Published online by Cambridge University Press: 24 February 2022
Euler’s striking proof of the fact that the infinite sum
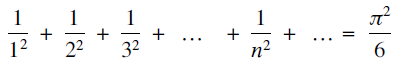 ${1 \over {{1^2}}}\, + \,{1 \over {{2^2}}}\, + \,{1 \over {{3^2}}} + \,...\, + \,{1 \over {{n^2}}} + \,...\, = {{{\pi ^2}} \over 6}$
${1 \over {{1^2}}}\, + \,{1 \over {{2^2}}}\, + \,{1 \over {{3^2}}} + \,...\, + \,{1 \over {{n^2}}} + \,...\, = {{{\pi ^2}} \over 6}$
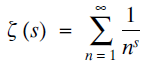 $\zeta (s)\zeta = \sum\limits_{n = 1}^\infty {{1 \over {{n^s}}}} $
, the above sum is rewritten as
$\zeta (s)\zeta = \sum\limits_{n = 1}^\infty {{1 \over {{n^s}}}} $
, the above sum is rewritten as 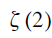 $\zeta (2)$
and the problem of its evaluation in closed form is often named after Basel - the city of Euler’s birth. Many solutions to the Basel problem exist today, with several original ones appearing on the pages of The Mathematical Gazette. The purpose of this Note is to present two short proofs, the first of which is a simplification of one in the literature and the second is believed to be new, of the equivalent fact that
$\zeta (2)$
and the problem of its evaluation in closed form is often named after Basel - the city of Euler’s birth. Many solutions to the Basel problem exist today, with several original ones appearing on the pages of The Mathematical Gazette. The purpose of this Note is to present two short proofs, the first of which is a simplification of one in the literature and the second is believed to be new, of the equivalent fact that
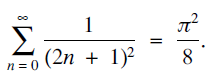 $\sum\limits_{n = 0}^\infty {{1 \over {{{(2n + 1)}^2}}} = {{{\pi ^2}} \over 8}} .$
$\sum\limits_{n = 0}^\infty {{1 \over {{{(2n + 1)}^2}}} = {{{\pi ^2}} \over 8}} .$