Another generalisation of Stewart's Theorem

Extract

The aim of this Article is to present a natural generalisation of a well-known result from plane geometry, called Stewart's Theorem. We will present our result in the Euclidean space 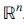, but we will prove it only for n = 3. Since its proof for n > 3 is involved, our intention is to give the details in another Article. A search in the relative literature returns many articles which generalise Stewart's Theorem in different directions. We first refer the reader to [1], where a collection of generalisations of Stewart's theorem is presented. In [2], two results are given, which describe a relation between k points in the Euclidean space 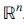and their weighted average. If we apply these theorems to the plane, we straightforwardly get Stewart's Theorem. Another result is given in [3], which is also reproduced in [1]. This result considers n + 1 points in 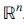which belong to a hyperplane U of dimension n − 1 and another point A ∉ U , and presents an interesting relation that combines distances between each of these points and A, hypervolumes of simplices and powers of points with respect to hyperspheres. Another relative result which involves convex quadrilaterals on the plane is proved in [4]. Lastly, in [5], a generalisation of [4] is proved for 2k points in 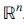, and a relation is found between distances of these points and the distance of two corresponding averages (of these points). These articles support the fact that there can be many interesting generalisations of Stewart's Theorem in different directions.