Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T07:07:40.156Z Has data issue: false hasContentIssue false
  • English
  • Français

Beyond the ratio test

Published online by Cambridge University Press:  17 October 2018

G. J. O. Jameson
G. J. O. Jameson*
Affiliation:
Dept. of Mathematics and Statistics, Lancaster University, Lancaster LA1 4YF e-mail: g.jameson@lancaster.ac.uk
Get access Rights & Permissions [Opens in a new window]

Extract

D'Alembert's ratio test, a very basic plank in the theory of infinite series, can be stated as follows:

Suppose that an > 0 for all n ≥ 1. Then:

  1. (i) if for some n0 and some ρ < 1, we have for all n ≥ n0, then 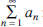is convergent;

  2. (ii) if for some n0, we have 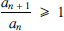for all n ≥ n0, then 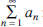is divergent.

Type
Articles
Information
The Mathematical Gazette , Volume 102 , Issue 555 , November 2018 , pp. 471 - 484
Copyright
Copyright © Mathematical Association 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Hyslop, J. M., Infinite series, Oliver and Boyd (1959).Google Scholar
2. Phillips, E. G., A course of analysis (2nd edn.), Cambridge (1939).Google Scholar
3. Ferrar, W. L., A textbook of convergence, Oxford University Press (1938).Google Scholar
4. Jameson, G. J. O., A fresh look at Euler's limit formula for the gamma function, Math. Gaz. 98 (July 2014) pp. 235–242.Google Scholar
5. Scott, J. A., On series for the Euler constant, Math. Gaz. 101 (November 2017) pp. 486–488.Google Scholar