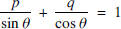As a youth entering the sixth form to study Mathematics, Further Mathematics and Physics I enjoyed the riches of the school's mathematics library and in particular three books which appealed to me, A mathematician's apology [1], A book of curves [2] and On growth and form [3].

Hardy's book [1] is one that an impressionable, young mathematician should not read unguided. It left me with the impression that the proper pursuit of mathematics was as a pure subject, of no use or application, to be studied for its own sake; to my regret, I held to this view for several years before finally being able to shake it off through teaching Newtonian mechanics. Looking across mathematics teaching today I seem to observe great interest in geometry, number and algebra ‘curiosities’ that are rooted entirely in mathematics. This in itself is no bad thing, since it clearly draws us and our students into the fascinating world of mathematics. But what of the applications of mathematics? Might they be equally fascinating? Surely we do not want to lure our students into Hardy's trap?

What is an axiom? The meaning of the term ‘axiom’ varies between different fields of study. In philosophy it means a statement that is accepted without argument, while in physics the term ‘postulate’ is used and it means a theory that was verified in an experiment, and will be considered as true unless it is disproved by other experiments.

In mathematics the notion of ‘axiom’ is used in two related but distinguishable meanings: ‘logical axioms’ and ‘non-logical axioms’. Logical axioms are certain statements that are always true, and from them all tautologies of the language can be derived. Non-logical axioms are statements that are taken to be true, to serve as a premise or starting point for further reasoning and arguments.

We can obtain a two-fold symmetric figure by folding a square sheet of paper in the middle and then cutting along some curves drawn on the paper. By making two perpendicular folds through the centre of the paper and then cutting, we can obtain a four-fold symmetric figure. We can also get an eight-fold symmetric figure by making a fold bisecting an angle made by the two perpendicular folds before cutting. But it is not possible to obtain a three-fold, five-fold or six-fold symmetric figure in this way; we need to make more folds before cutting. Making a three-fold (respectively five-fold and six-fold) figure involves the division of the angle at the centre (360°) of a square sheet of a paper into six (respectively ten and twelve) equal parts. In other words, we need to construct the angles 60°, 36° and 30°. But these angles cannot be obtained by repeated bisections of 180° by simple folding as in the making of two-fold, four-fold and eight-fold figures. In [1], we see that each of the constructions of 60° and 30° applies the fact that sin 30° = ½ and takes only a few simple folding steps. The construction of 36° is more tedious (see, for example, [2] and [3]) as sin 36° is not a simple fraction but an irrational number. In this Article, we show how to make, by paper-folding and cutting a regular pentagon, a five-pointed star and create any five-fold figure as we want. The construction obtained by dividing the angle at the centre of a square paper into ten equal parts is called a pentagon base. We gained much insight from [2] and [3] when developing the method for making the pentagon base to be presented below.

The main goal of this paper is to give a deeper understanding of the geometrical inequality proposed by Martin Lukarevski in [1]. In order to formulate our results we shall introduce and use the following notation throughout this paper. Let A1A2A3 be a triangle a1, a2, a3, the lengths of the sides opposite to A1, A2, A3 respectively, P an arbitrary inner point of it xi, the distance of P from the side of length ai. Let r, R be the inradius and circumradius of the triangle hi, the altitude belonging to side ai, Δ the area and finally let α be a real parameter. We adopt also the use of Σui to refer the sum taken over the suffices i = 1, 2, 3. Now we are in the position to reformulate the original problem into a more general form namely: find bounds for Σxαi in terms of r and R. The main results of our investigation are summarised in the following theorem.

Difference equations have a wide variety of applications, including fluid flow analysis, wave propagation, circuit theory, the study of traffic patterns, queueing analysis, diffusion theory, and many others. Besides these applications, studies into the analogy between ordinary differential equations (ODEs) and difference equations have been a favourite topic of mathematicians (e.g. see [1] and [2]). These applications and studies bring to light the similar character of the solutions of a difference equation with a fixed step size and a corresponding ODE.

Also, an important numerical technique for solving both ordinary and partial differential equations (PDEs) is the method of finite differences [3], whereby a difference equation with a small step size is utilised to obtain a numerical solution of a differential equation. In this paper, elements of both of these ideas will be used to solve some intriguing problems in pure and applied mathematics.

The quadratic equation is a central topic in high school algebra. It provides the simplest generalisation of the familiar linear equation, and finding its roots introduces students to a non-trivial problem that requires the application of new techniques, such as completing the square and/or factorisation into linear factors involving the roots. It also introduces the student to the phenomenon of repeated roots, which opens the door to a discussion of multiplicities of roots. Furthermore, it naturally exposes the student to the case where the equation has no real roots, a phenomenon that could also be used to introduce the student to complex numbers.

Magic: the gathering is a trading card game published by Wizards of the Coast [1]. The aim of most variants of the game is to reduce your opponent's life total from twenty to zero, thus winning the game. As it may take several turns to reduce a player's life total to zero, players need a mechanism to keep track of their current life total. For this purpose, players often use a device called a spindown life counter, shown in Figure 1. A spindown life counter is an icosahedron with a special labelling of the faces, such that − starting with 20 life total − a player can reduce their life total in decrements of one by rolling the icosahedron onto an adjacent face each time. A spindown life counter appears similar to a standard icosahedral die, known in gaming as a d20; however, the labelling of faces is different, as also shown in Figure 1.

The title of this Article pays homage to Greg Frederickson's widelyknown book on geometrical dissections, Dissections: Plane & Fancy [1]. I enjoyed the book so much, I built an honours geometry course around it − a terminal mathematics course for honours students needing a mathematics credit for their general education requirements. Not only is there significant geometry involved, but there is a fair amount of number theory relevant to finding infinite families of dissections of, for example, m squares to n squares.

However, although many dissections from one regular polygon to another are quite elegant, the mathematics involved in specifying the dissections is often formidable.

The circles C1, … , Cn form a chain of length n, or an n-chain, if Ci touches Ci + 1, for i = 1, … , n − 1, and the chain is closed if also Cn touches C1. If Ci touches Ci + 1 at Qi, for i = 1, … , n (subscripts being interpreted modulo n), then Q1, … , Qn (assumed distinct) are the contact points of the chain. A cyclic chain is a chain for which all the circles touch another circle S, the base circle of the chain, and if Ci touches S at Pi, then P1, … , Pn are the base points of the chain.

D'Alembert's ratio test, a very basic plank in the theory of infinite series, can be stated as follows:

Suppose that an > 0 for all n ≥ 1. Then:

1. (i) if for some n0 and some ρ < 1, we have for all n ≥ n0, then is convergent;

2. (ii) if for some n0, we have for all n ≥ n0, then is divergent.

Mathematicians know that the path from adolescent competence to adult professional life is full of unexpected twists and turns, and is fraught with potential pitfalls. Even when faced with very able adolescents, it is not at all clear which of them will flourish in the long run, or how one can best support their future development (when they eventually become young adults) in a way that takes their mathematical ability and inclinations seriously – whether in pure or applied mathematics, in computer science or software development, in engineering, mathematical biology, financial mathematics or linguistics, in management, or in some totally different profession.