Hostname: page-component-cd9895bd7-8ctnn Total loading time: 0 Render date: 2024-12-26T06:36:09.104Z Has data issue: false hasContentIssue false
  • English
  • Français

Equal sums, sums of squares and sums of cubes

Published online by Cambridge University Press:  24 February 2022

G. J. O. Jameson
G. J. O. Jameson*
Affiliation:
13 Sandown Road, LancasterLA1 4LN e-mail: pgjameson@talktalk.net
Get access Rights & Permissions [Opens in a new window]

Extract

Consider the problem of finding triples of numbers (x1, x2, x3) and (y1, y2, y3) satisfying (1)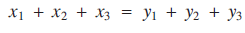

$${x_1} + {x_2} + {x_3} = {y_1} + {y_2} + {y_3}$$
and (2)
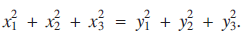$$x_1^2 + x_2^2 + x_3^2 = y_1^2 + y_2^2 + y_3^2.$$

Type
Articles
Information
The Mathematical Gazette , Volume 106 , Issue 565 , March 2022 , pp. 54 - 60
Check for updates
Copyright
© The Authors, 2022. Published by Cambridge University Press on behalf of The Mathematical Association

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Jameson, G. J. O., Monotonicity of the mid-point and trapezium estimates for integrals, Math. Gaz. 105 (November 2021) pp. 433–441.10.1017/mag.2021.110CrossRefGoogle Scholar
Jameson, G. J. O., Counting zeros of generalised polynomials: Descartes’ rule of signs and Laguerre’s extensions, Math. Gaz. 90 (July 2006) pp. 223–234.10.1017/S0025557200179628CrossRefGoogle Scholar