Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T06:55:54.057Z Has data issue: false hasContentIssue false
  • English
  • Français

Folding a triangle

Published online by Cambridge University Press:  23 January 2015

Andrew Jobbings
Andrew Jobbings*
Affiliation:
4 West Avenue, Baildon, Shipley BD17 5HA
Get access Rights & Permissions [Opens in a new window]

Extract

The Original problem

Take a right-angled triangle ABC, where ∠C = 90°, and fold along UV so that C lies on AB, as shown in Figure 1, where C' is the new position of C.

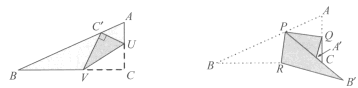
Problem: Where should one fold in order to minimise the area of the folded triangld CUV?

This problem was discussed by Hirschhom in [1], where he gives its origins and provides a solution, describing the answer as ‘quite remarkable’. However, he does not relate the answer to the geometry of the configuration. We adopt a more geometrical approach and use some simple folding ideas—there is a close relationship between paper folding and geometry which deserves to be more widely known (see [2] for example).

Type
Articles
Information
The Mathematical Gazette , Volume 97 , Issue 539 , July 2013 , pp. 210 - 217
Copyright
Copyright © The Mathematical Association 2013

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Hirschhorn, Michael D., A triangle-folding problem, Math. Gaz. 95 (November 2011) pp. 514–517.Google Scholar
2. Geretschlliger, Robert, Geometric origami, Arbelos (2008).Google Scholar
3. Loy, Jim, Trisection of an angle. url: http://www.jimloy.com/geometry/trisect.htm Google Scholar
4. Verrill, Helena, Origami trisection of an angle. url: http://www. math.lsu.edu/~verrill/origami/trisect/ Google Scholar