Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-25T06:57:55.914Z Has data issue: false hasContentIssue false
  • English
  • Français

A geometric proof of the binomial identity

Published online by Cambridge University Press:  12 November 2024

František Marko  and
Semyon Litvinov
František Marko
Affiliation:
The Pennsylvania State University, 76 University Drive, Hazleton, PA 18202, USA e-mails: fxm13@psu.edu,snl2@psu.edu
Semyon Litvinov
Affiliation:
The Pennsylvania State University, 76 University Drive, Hazleton, PA 18202, USA e-mails: fxm13@psu.edu,snl2@psu.edu
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We give a geometric proof of the binomial identity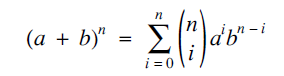 for all natural n and real a,b. This work was inspired by the book [1], where the binomial identity for n = 3 and a,b > 0 is proved by breaking a cube C of size (a + b) × (a + b) × (a + b) into eight rectangular boxes and counting their volumes as follows.

Type
Articles
Information
The Mathematical Gazette , Volume 108 , Issue 573 , November 2024 , pp. 430 - 436
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (https://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Authors, 2024 Published by Cambridge University Press on behalf of The Mathematical Association

References

Banchoff, Thomas F., Beyond the third dimension, Scientific American Library (1996).Google Scholar
Inclusion–exclusion principle, Wikipedia, accessed March 2024 at https://en.wikipedia.org/wiki/Inclusion-exclusionprincipleGoogle Scholar