Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T12:18:49.787Z Has data issue: false hasContentIssue false
  • English
  • Français

Integral powers of order three Latin square matrices

Published online by Cambridge University Press:  01 August 2016

N. Gauthier
N. Gauthier*
Affiliation:
Department of Physics, The Royal Military College of Canada, PO Box 17 000, Station Forces, Kingston, ON K7K 7B4 Canada
Get access Rights & Permissions [Opens in a new window]

Extract

An order-n Latin square contains numbers, each of which is one of a set of n real numbers, 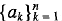, arranged in the form of an n × n matrix, in such a way that each row and each column of the matrix contains all n numbers. Euler (1707-1783) was the first to study the properties of Latin squares and they have been the focus of continued attention since. Studies of Latin squares naturally lead one to elements of group theory and of matrix theory. As will be shown in this note, both of these features may offer interesting investigative opportunities for classroom discussions of the permutation group on three symbols and of the algebra of the associated permutation matrices.

Type
Articles
Information
The Mathematical Gazette , Volume 93 , Issue 526 , March 2009 , pp. 42 - 50
Copyright
Copyright © The Mathematical Association 2009

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Emanouilidis, E., Powers of Latin squares, Math. Gaz. 90 (November 2006) pp. 478–481.CrossRefGoogle Scholar
2. Emanouilidis, E. and Bell, R., Latin squares and their inverses, Math. Gaz. 88 (March 2004) pp. 127–128.CrossRefGoogle Scholar
3. Trenkler, G. and Trenkler, D., On singular 3x3 semi-diagonal Latin squares, Math. Gaz. 91 (March 2007) pp. 126–128.CrossRefGoogle Scholar
4. Abramowitz, M. and Stegun, I. A., Handbook of Mathematical Functions, Dover Publications, New York (1972), 9th printing, p. 823, sections 24.1.1 (binomial expansion) and 24.1.2 (multinomial expansion).Google Scholar
5. Dixon, J. D. and Mortimer, B., Permutation Groups, Springer-Verlag, New York (1996).CrossRefGoogle Scholar
6. Goodman, R. and Wallach, N. R., Representations and Invariants of the Classical Groups, in Rota, G.-C. (ed.), Encyclopedia of mathematics and its applications, vol. 68. Cambridge University Press, Cambridge (1998), section 2.5.Google Scholar
7. Banchoff, T. and Wermer, J., Linear algebra through geometry, Springer-Verlag, New York (1983), pp. 141–144.CrossRefGoogle Scholar