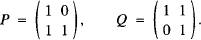Articles
A new look at Eddington's liar problem
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 1-9
-
- Article
- Export citation
The hyperexponential function
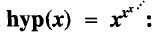 an exercise in convergence
an exercise in convergence
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 193-199
-
- Article
- Export citation
A Manifesto for Mathematics
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 385-397
-
- Article
- Export citation
Other
Index to the Mathematical Gazette
-
- Published online by Cambridge University Press:
- 21 September 2016, pp. i-viii
-
- Article
- Export citation
Articles
Reflected circles, and congruent perspective triangles
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 10-26
-
- Article
- Export citation
Front Matter
MAG volume 93 issue I1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 01 August 2016, p. f1
-
- Article
- Export citation
Articles
The frog problem: more than you might want to know
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 398-403
-
- Article
- Export citation
On a simple set of integers
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 200-212
-
- Article
- Export citation
Groups associated with conics
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 27-41
-
- Article
- Export citation
Pseudoperfect numbers with no small prime divisors
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 404-409
-
- Article
- Export citation
Relation between work in two inertial frames
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 213-221
-
- Article
- Export citation
Integral powers of order three Latin square matrices
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 42-50
-
- Article
- Export citation
Optimal strategies for the progressive Monty Hall problem
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 410-419
-
- Article
- Export citation
More interlinked loops
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 222-227
-
- Article
- Export citation
Geoboards, polygons and Pick’s Theorem
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 228-231
-
- Article
- Export citation
Conjugation 2: Conjugate lines in a triangle
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 420-432
-
- Article
- Export citation
The sequence of n-dimensional cube-fractals
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 51-57
-
- Article
- Export citation
Conjugation 1 – Conjugate points in a triangle
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 232-236
-
- Article
- Export citation
A jigsaw problem
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 58-65
-
- Article
- Export citation
Prime matrices and prime polynomials
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 433-440
-
- Article
- Export citation

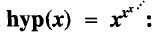 an exercise in convergence
an exercise in convergence

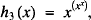 x appearing 3 times,
x appearing 3 times, x appearing 5 times.
x appearing 5 times.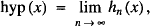


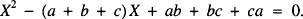
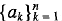 , arranged in the form of an
, arranged in the form of an 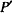 (
(