In 1942, R. C. Lyness noted that some recurrence relations generate cycles, irrespective of the initial values. For example, the order 2 recurrence relation

generates a cycle of period 5 for almost all values of u1 and u2 [1].

The globally periodic nature of sequences generated by this recurrence relation can be seen by setting u1 = x and u2 = y. The sequence is then

Lyness gave other examples of such recurrence relations but had been unable to find one with period 7 and challenged readers of the Gazette to find such a recurrence relation or prove it to be impossible.

No answer to this challenge was forthcoming. However, since Lyness's time, interest in these cycles has been maintained due to links with cross-ratios and elliptic curves. In recent years, Jonny Griffiths has done much to popularise these cycles [2].

We will prove a generalisation to our Theorem 10 about duality between orthodiagonal quadrilaterals and equidiagonal quadrilaterals in [1, p. 134]. These are quadrilaterals with perpendicular diagonals and diagonals of equal lengths respectively. Unfortunately we made a careless mistake in the proof of Theorem 10 (ii) in [1], which was found by Zoltán Szilasi at the University of Debrecen in Hungary. When reviewing that theorem, we realised that it's just a special case of a more general theorem. The equilateral triangles in Theorem 10 can be replaced by almost any regular polygons.

The general class of quadrilaterals where one diagonal is bisected by the other diagonal has appeared very rarely in the geometrical literature, but they have been named several times in connection with quadrilateral classifications. Günter Graumann strangely gave these objects two different names in [1, pp. 192, 194]: sloping-kite and sliding-kite. A. Ramachandran called them slant kites in [2, p. 54] and Michael de Villiers called them bisecting quadrilaterals in [3, pp. 19, 206]. The latter is a pretty good name, although a bit confusing: what exactly is bisected?

We have found no papers and only two books where any theorems on such quadrilaterals are studied. In each of the books, one necessary and sufficient condition for such quadrilaterals is proved (see Theorem 1 and 2 in the next section). The purpose of this paper is to investigate basic properties of convex bisecting quadrilaterals, but we have chosen to give them a slightly different name. Let us first remind the reader that a quadrilateral whose diagonals have equal lengths is called an equidiagonal quadrilateral and one whose diagonals are perpendicular is called an orthodiagonal quadrilateral.

In an earlier issue of the Mathematical Gazette, Nick Lord established the familiar formula for the sum of the first n squares using a physical argument based on the centroid of a configuration of masses in the plane [1]. In [2] we demonstrate an alternative configuration that gives the same result. This article is a follow-up to these papers, in which we find physical derivations of the formula for

for each k ∈ {1, 2, 3, 4, 5}. Let us first summarise the required theory. Take any region X ⊆ ℝ2 with uniform density and total area A. The centroid of is the arithmetic mean position of all of the points in X. If a region has a line of symmetry then the centroid will be located on that line.

As usual, write

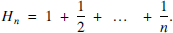
In [1], it is shown, by an elegant method, that for all n ⩾ 2, Hn is not an integer. The method can be traced back at least to [2, Exercise 251, p. 159]. Actually, rather more is shown: if Hn is expressed as a fraction an/bn in its lowest terms, then for all n ⩾ 2, bn is even. One way of looking at this is to say that once the term 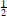has entered the sum, the factor 2 persists in the denominator from then on. This suggests the following question:

(Q1) for primes p ⩾ 3, is bn a multiple of p for all n ⩾ p?

and more generally:

(Q2) for any prime p, is bn a multiple of pm for all n ⩾ pm?

In other words, once 1/pm has entered the sum, does the factor pm persist in the denominator?

Let dn denote the lowest common multiple of 1, 2, … , n. This number can be described as follows: for each prime p ⩽ n, let mp be the largest integer m such that pm ⩽ n. Then 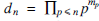. Hence a positive answer to (Q2) would imply that bn simply equals dn.

There have been numerous attempts to model the governing dynamics between the two ostensibly competing concepts of brilliance and mechanical steadiness. One interesting study is given by the English mathematician G. H. Hardy in his model [1] describing two characteristically different golfers playing a match against each other. The model challenges the apparently accepted doctrine of the ‘Brilliant player’ having the advantage over the ‘Steady player’ in a long series of golf matches by holes. Hardy defines ‘brilliance’ as the capacity to produce ingenious results as well as the capacity to make mistakes, compared to ‘steadiness’ being completely mechanical producing the same average result all the time. The two players in his model are equal in performance on average, only the brilliant player has a higher standard deviation whereas the consistent player has a standard deviation of 0.

Integration is an important topic discussed in first year calculus. Many subsequent topics, such as solving first-order or second-order differential equations, requires the evaluation of at least one integral, and sometimes several.

The most challenging material in integration is arguably the techniques of integration. Unfortunately, due to time constraints, only basic techniques are commonly taught, while in reality, many integrals having special forms are solvable only by using more sophisticated techniques.

In the performance of digital communication systems over fading channels, the error analysis is typically modelled using a Gaussian probability distribution. One function central to the analysis is what engineers routinely refer to as the (Gaussian) Q-function and is defined by

1

This is the canonical representation used for the function. In this paper a number of derivations of an important alternative representation for the Q-function known as Craig's formula will be given.

In 1879, the Irish astronomer Robert Stawell Ball published a slim book entitled simply Mechanics [1]. This book appeared as part of the series of ‘London Science Class-Books’, published by Longmans, Green & Co. These books were intended as elementary science texts for use in schools, and, as a consequence, their mathematical content was quite basic — even for those books on supposedly mathematical topics. In this article, I will look at Ball's handling of his subject, and compare his book to its distant ancestor: Newton's Principia.