Obituary
Oughtred’s “Clavis”
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 161
-
- Article
-
- You have access
- Export citation
Research Article
An Extended Use of Velocity-Time Graphs
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 162-168
-
- Article
- Export citation
Other
Gleanings Far and Near
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 168
-
- Article
- Export citation
Article Commentary
On Cartophily and Motor Cars
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 169-171
-
- Article
- Export citation
Research Article
The Euler-Maclaurin Formula
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 172-176
-
- Article
- Export citation
On the Multiplication of Complex Numbers
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 177-179
-
- Article
- Export citation
Other
Non-Certificate Mathematics*
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 180-186
-
- Article
- Export citation
Mathematical Teaching in Other Lands
Teaching of Mathematics in Australia
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 187-189
-
- Article
- Export citation
Basic Considerations in the Teaching of Mathematics in the High Schools of the U.S.A.
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 189-196
-
- Article
- Export citation
Other
Mathematical Schoolbooks in Switzerland
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 197-201
-
- Article
- Export citation
On Differentials
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 202-204
-
- Article
- Export citation
The Energy of Fluids in Motion
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 205-207
-
- Article
- Export citation
Mathematical Notes
2057 Sign in relation to curvature (XXVII, No. 274, p. 77, May, 1943, and XXVIII, No. 282, p. 185, Note 1754, December, 1944)
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 208-211
-
- Article
- Export citation
2058. A property of the cyclic quadrilateral
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 211
-
- Article
- Export citation
2059. Loss of energy on impact
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 211-212
-
- Article
- Export citation
2060. The vector triple product
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 212
-
- Article
- Export citation
2061. A geometrical proof of a problem in algebra
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 212-213
-
- Article
- Export citation
2062. A proof of the product rule for determinants
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 213-214
-
- Article
- Export citation
2063. A question of hats
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 214-215
-
- Article
- Export citation
2064. On Notes 1542, 1801, 1843
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 215
-
- Article
- Export citation

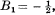 all other B with odd subscripts vanish, and those with even subscripts are alternately positive and negative.
all other B with odd subscripts vanish, and those with even subscripts are alternately positive and negative. 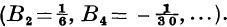 We shall often ignore the fact that
We shall often ignore the fact that