It is perhaps a rather unfortunate and possibly misleading fact that the standard list of theorems in geometry contains two which are specially labelled “Theorems on Loci” and form a section to themselves, viz. Section 3 in the I.A.A.M. schedule. It is liable to suggest that the notion of a locus and the properties of loci form an isolated subject like a chapter, say, on quadratic equations, which do not concern us until we reach it, and when this moment arrives we have merely to do our two theorems and a few examples and then may regard the subject as disposed of and consider no further reference is needed except possibly in a revision of proofs of theorems before taking School Certificate.

In a previous paper we considered fractional integration and differentiation of functions of a real variable. In the present paper the complex variable will be used.

We define a λth integral, or a (−λ)th differential coefficient, of f(z) along a simple curve l by

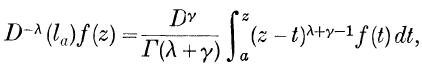
where the integration and differentiation are along l, starting from a, λ is any number, real or complex, γ is the least integer greater than or equal to zero such that R(λ) + γ > 0, R(λ) being the real part of λ; and D stands for 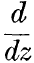, denoting differentiation along l. a is arbitrary and independent of z, and in the present paper is to be taken as finite.

This interesting solid has tended too much in the past to be classified as “for adults only” (and for not too many of them); but because it supplies the answer to a question which every intelligent youngster asks himself, I think it is worth while to try and smooth the path of any teacher who wants to let children of (say) 13 share in some of its treasures.

The usual method of developing the theory of the exponential and logarithmic functions is to take as a definition either

or

The first definition has the disadvantage that with it a good deal of the theory of series is needed. Neither development follows the lines on which the student first met the functions. A good deal could be said for the view that for most students the best type of accurate theory is one which fills up the gaps in methods which are already familiar The difficulties of taking

as a definition are well known.

By a space of n dimensions we mean a region in which the position of a given point is determined by n independent coordinates. If the region is such that the shortest distance between any two given points is the straight line joining them, the space is termed flat, the geometry of a flat space is akin to that of the plane as contrasted with, say, spherical geometry For brevity, a flat space of n dimensions will be denoted by the symbol [n].