Other
Annual Meeting of the Mathematical Association, 1938
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 177
-
- Article
- Export citation
Research Article
Logarithms by Interpolation*
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 177-181
-
- Article
- Export citation
Other
Gleanings Far and Near
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 181-225
-
- Article
- Export citation
Research Article
The Solution of Equations by the use of Proportional Differences
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 182-187
-
- Article
- Export citation
Theorems on the Tetrahedron
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 188-202
-
- Article
- Export citation
A Simple Geometrical Device, and Some of its Applications
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 203-209
-
- Article
- Export citation
On the Representation of Circles by means of Points in Space of Three Dimensions
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 210-215
-
- Article
- Export citation
Fractional Calculus
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 216-219
-
- Article
- Export citation
The Theory of Complex Numbers*
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 220-225
-
- Article
- Export citation
Mathematical Notes
1242. Note on integration
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 226-228
-
- Article
- Export citation
1243. On the relation of an analytic function of z to its real and imaginary parts
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 228-229
-
- Article
- Export citation
1244. A note on Bessel's function of order zero
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 229-230
-
- Article
- Export citation
1245. A note on x2 + y2=N
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 230
-
- Article
- Export citation
1246. A proof of an elementary theorem in geometry
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 231
-
- Article
- Export citation
Reviews
Relativity Theory of Protons and Electrons. By Sir A. S. Eddington. Pp. vi, 336. 21s. 1936. (Cambridge)
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 232-236
-
- Article
- Export citation
Geschichte der Elementar-Mathematik in systematischer Darstellung mit besonderer Berücksichtigung der Fachwörter. III. Proportionen, Gleichungen. By J. Tropfke. Third edition. Pp. 239. RM. 10. 1937. (Walter de Gruyter, Berlin and Leipzig)
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 236-237
-
- Article
- Export citation
An Illustrated Historical Time Chart of Elementary Mathematics for Senior and Secondary Schools, Training Colleges and Universities. By E. J. Edwards. Five charts, thick cardboard, varnished. 21s. 1936. (University of London Press)
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 237-239
-
- Article
- Export citation
The Collected Works of George Abram Miller. Volume I. Pp. xi, 475. $7.50. 1935. (University of Illinois Press)
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 239-240
-
- Article
- Export citation
Einführung in die analytische Geometrie und Algebra. II. By O. Schreier and E. Sperner. Pp. 308. Geh. RM. 6; Geb. RM. 7.20. 1935. Hamburger Mathematische Einzelschriften, 19. (Teubner)
-
- Published online by Cambridge University Press:
- 03 November 2016, pp. 240-241
-
- Article
- Export citation
Dynamics. Part II. By A. S. Ramsey. Pp. xi, 344. 15s. 1937. (Cambridge University Press)
-
- Published online by Cambridge University Press:
- 03 November 2016, p. 241
-
- Article
- Export citation

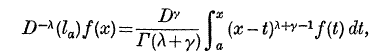
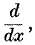 and
and