We tackle an unusual problem that, as far as I know, is not in the standard literature. To state it concisely I use what I call ‘valid sets’. We know that in any three or more positive quantities, only the largest can be half or more of the total value; and is then obviously greater than the sum of all the others. But if the largest is less than half the total of the set, it must be less than the sum of the others; and this is true for every element in this set. I call such a set ‘valid’. For example, the sides of a triangle are valid, as are the face areas of a tetrahedron. Our problem relates to the converse for a tetrahedron: given any four valid quantities, is there always a tetrahedron with those face areas? In this article I answer this by showing that, for any valid set, we can always construct the net of a corresponding tetrahedron. In fact, for any given valid set there is always an infinity of non-congruent tetrahedra with the given face areas. Although in general there are no formulae that give the exact edge lengths of these solids, I show that there are always several distinct infinite subsets that are constructible and whose edge lengths can be determined exactly.
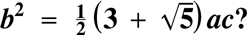 ${b^2} = \frac{1}{2}\left( {3 + \sqrt 5 } \right)ac$
${b^2} = \frac{1}{2}\left( {3 + \sqrt 5 } \right)ac$
 $\sqrt 2$ with determinants
$\sqrt 2$ with determinants