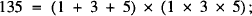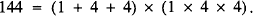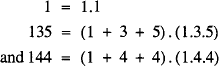Editorial
The Fourth Annual Mathematical Gazette Writing Awards
-
- Published online by Cambridge University Press:
- 01 August 2016, p. 193
-
- Article
-
- You have access
- Export citation
Other
Index to the Mathematical Gazette
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. i-xiv
-
- Article
- Export citation
Articles
Something interesting! The 1999 Presidential Address
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 386-393
-
- Article
- Export citation
Editorial
Editorial: It’s voting time again!
-
- Published online by Cambridge University Press:
- 01 August 2016, p. 1
-
- Article
-
- You have access
- Export citation
Articles
What goes round comes round
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 394-399
-
- Article
- Export citation
The origin of Ferrers graphs
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 194-198
-
- Article
- Export citation
Front Matter
MAG volume 83 issue I1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 01 August 2016, p. f1
-
- Article
- Export citation
Articles
Principle of the extreme element
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 2-9
-
- Article
- Export citation
What shape is an ellipse?
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 400-409
-
- Article
- Export citation
Anyone for tennis?
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 199-209
-
- Article
- Export citation
Stanisław Ulam 1909-1984
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 10-24
-
- Article
- Export citation
An exploration of hyperpower equations nx = ny
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 210-215
-
- Article
- Export citation
Families of ovals and their orthogonal trajectories
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 410-420
-
- Article
- Export citation
S•P numbers*
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 25-32
-
- Article
- Export citation
Simple mappings in mechanics
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 421-425
-
- Article
- Export citation
There are only three S•P numbers!
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 32-38
-
- Article
- Export citation
Moving the first digit of a positive integer to the last
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 216-220
-
- Article
- Export citation
Solitary Solarians and densely packed spheres - from Stephen Hales to Thomas Hales
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 426-432
-
- Article
- Export citation
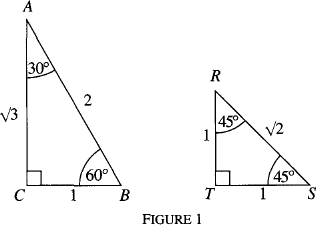
Triangles, surds and pell’s equation
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 221-225
-
- Article
- Export citation
Partitions into square-pairs
-
- Published online by Cambridge University Press:
- 01 August 2016, pp. 39-46
-
- Article
- Export citation