Given a differentiable function f with argument x, its critical points are those values of x, if any, in its domain for which either f′ (x) = 0 or f′ (x) is undefined. The first derivative test is a number line test that tells us, definitively, whether a given critical point, x = c, of f(x) is a local maximum, a local minimum, or neither. The second derivative test is not a number line test, but can also be applied to classify the critical points of f(x). Unfortunately, the second derivative test is, under certain conditions, inconclusive.
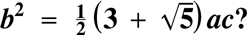 ${b^2} = \frac{1}{2}\left( {3 + \sqrt 5 } \right)ac$
${b^2} = \frac{1}{2}\left( {3 + \sqrt 5 } \right)ac$