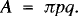It is widely, almost universally, believed that the Hebrew Bible gives the value of π as the crude approximation 3, a value much less accurate than those adopted by other ancient civilisations, such as the Babylonian, the Egyptian and the Chinese. In the English of the Authorised Version, the biblical source goes:

‘And he made a molten sea, ten cubits from one brim to the
other: it was round all about, and his [i.e. its] height was five
cubits: and a line of thirty cubits did compass it round about.’

What are your mathematical gems? Which results or ideas in mathematics give you the greatest pleasure? Which of them would you choose to take with you to while away the hours on a desert island? Is there a mathematical book above all others that you would wish to have with you? How would you make your choices? And what would be the reason for each specific choice? Similar questions are asked of celebrities (and noncelebrities to boot) in a long-running and very popular radio programme in Britain called Desert Island Discs. The difference is that the radio guests are asked to choose a number of pieces of music, together with one book (other than the Bible or Shakespeare, which are routinely provided), and one luxury.

In tackling a problem, we needed to show that a certain 3 × 3 determinant is non-zero. This determinant could be expressed in terms of the symmetric, homogeneous function N = Σx.Σx2 + 6xyz - 2Σx3 of three variables, where, for example Σx2 = x2 + y2 + z2. We first looked into several classical books, to see if there was a relevant inequality. There was not, nor do they contain anything other than ad hoc techniques for dealing with the inequalities they give. In this paper we give a general method for dealing with a certain class of such inequalities; it might be instructive for undergraduates, partly to exercise them in applying a moderately complicated algorithm, and partly to show an application of 2- and 3- variable Calculus.

This paper contains many opportunities to investigate, conjecture and verify results by writing simple computer programs, and the reader is strongly urged to participate in this way throughout.

For each positive integer n, let F(n) be the sum of the squares of the digits of n; for example,

According to Richard Courant and Herbert Robbins writing more than fifty years ago in their classic book What is Mathematics? (which is still in print)

Sadly for many students entering university with A level Mathematics, and for some leaving university with a degree in Mathematics, this is not so. As was noted by John Smith, for some students there appears to be little understanding of the principles.

While reading a book by David Wells on curious and interesting geometry, I came across the following remarkable theorem named after Holditch.

In Figure 1 the point R divides a straight stick ST into lengths p and q, where p, q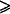 0. We restrict the end points of the stick, S and T, to lie on a plane, simple, closed, convex contour, C1, and ST slides around C1. Assuming C1 is such that ST can pass around C1 once, the locus of R is another plane closed contour, C, inside C1.

In an earlier note the iterative behaviour of taking the unit imaginary, i, to higher and higher powers of i was described. This iterative power sequence converged to a limit. In order to make discussion of later developments simpler we need to introduce some definitions.

In this article we set up a mathematical model to represent the effects of the forces which operate during the rowing of racing shells. The analysis is conducted in terms of eights, but could apply equally well to fours, pairs and double or quad sculls, and even (with obvious verbal changes) to single sculls. McMahon as well as McMahon and Bonner have previously considered various numbers of rowers in racing shells, and reached conclusions suggesting that consideration of an eight is representative of all possible combinations of rowers.

Two days before his death in the summer of 1901 Peter Guthrie Tait gave his son some handwritten notes on quaternions for safekeeping. Though he had distinguished himself in many areas of mathematical physics and had influenced the work of Thomson and Maxwell it was his evangelical promotion of quaternions which would be remembered in the years to follow and it was fitting that his last energies be devoted to the cause.

In Euclidean plane geometry there exists an interesting, although limited, duality between the concepts angle and side, similar to the general duality between points and lines in projective geometry. Perhaps surprisingly, this duality occurs quite frequently and is explored fairly extensively in.

The square is self-dual regarding these concepts as it has all angles are equal, as well as all its sides.

It is well known that as I was trying to illustrate this to some students by calculating and so on, using the ‘story’ about a sum of £1 invested at 100% interest. After one year this would yield £2 if interest is added annually, £2.25 if added (compounded) at each half-year, £2.37 if compounded every 4 months, and so on.

In this article I investigate Napoleon triangles, generalisations of the mysterious equilateral triangle in Napoleon’s theorem. I start with that theorem, develop some analogous results, find configurations with unexpected integer angles, and return to an extension of Napoleon’s theorem. Many of the geometrical proofs depend upon spiral similarities, and the numerical work uses some unfamiliar trigonometrical identities.

In a recent Note Nick Lord proved that if a polynomial f(x) of degree n takes prime values for 2n + 1 integer values of x, then it is irreducible. (All polynomials discussed here are assumed to have integer coefficients and, like Lord, I regard numbers of the form –p where p is a positive prime as primes in their own right.) He wondered whether his result is the best possible one of its kind. If we restrict attention to positive primes, a best possible result can be achieved (Theorems 2 and 3 below). When we allow negative primes, Lord's result can be improved (see Theorems 1, 3 and 4) by an observation which still surprises me.

There has always been a mystery about how Kepler (1571-1630) discovered the laws of planetary motion: not until more than half a century later did Newton show how they can be explained within a gravitational framework. It is generally assumed that Kepler based his achievements on the full panoply of classical Greek geometry, and certainly he was very familiar with the advanced techniques developed by Archimedes and Apollonius, which he often referred to in his optical and stereometrical work. Yet I have found that for his astronomical success Kepler relied on nothing more complicated than the methods and results of Euclid. And since he did not know what sort of solution his enquiry would produce, my historical account of Kepler's discovery turns into a tale of detection – which began at the University of Tübingen in the early 1590s.