Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T21:10:53.511Z Has data issue: false hasContentIssue false
  • English
  • Français

Counting and equidistribution in quaternionic Heisenberg groups

Part of: Multiplicative number theory Linear algebraic groups and related topics Forms and linear algebraic groups Discontinuous groups and automorphic forms Global differential geometry

Published online by Cambridge University Press:  08 July 2021

JOUNI PARKKONEN  and
FRÉDÉRIC PAULIN
JOUNI PARKKONEN
Affiliation:
Department of Mathematics and Statistics, P.O. Box 35, 40014 University of Jyväskylä, Finland. e-mail: jouni.t.parkkonen@jyu.fi
FRÉDÉRIC PAULIN
Affiliation:
Laboratoire de Mathématique d’Orsay, UMR 8628 CNRS, Université Paris–Saclay, 91405 ORSAY Cedex, France, e-mail: frederic.paulin@universite-paris-saclay.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

We develop the relationship between quaternionic hyperbolic geometry and arithmetic counting or equidistribution applications, that arises from the action of arithmetic groups on quaternionic hyperbolic spaces, especially in dimension 2. We prove a Mertens counting formula for the rational points over a definite quaternion algebra A over 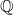${\mathbb{Q}}$ in the light cone of quaternionic Hermitian forms, as well as a Neville equidistribution theorem of the set of rational points over A in quaternionic Heisenberg groups.

MSC classification

Primary: 11F06: Structure of modular groups and generalizations; arithmetic groups 11N45: Asymptotic results on counting functions for algebraic and topological structures 20G20: Linear algebraic groups over the reals, the complexes, the quaternions 53C55: Hermitian and Kählerian manifolds
Secondary: 11E39: Bilinear and Hermitian forms 53C17: Sub-Riemannian geometry 53C22: Geodesics
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 173 , Issue 1 , July 2022 , pp. 67 - 104
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

D., Allcock. New complex- and quaternion-hyperbolic reflection groups. Duke Math. J. 103 (2000), 303–333.Google Scholar
Y., Benoist and J.-F., Quint. Stationary measures and invariant subsets of homogeneous spaces II. J. Amer. Math. Soc. 26 (2013), 659–734.Google Scholar
M., Berger, P., Gauduchon and E., Mazet. Le spectre d’une variété riemannienne. Lecture Notes Math. 194 (Springer Verlag, 1971).CrossRefGoogle Scholar
O., Biquard. Quaternionic contact structures. Proceedings of the Second Meeting on Quaternionic Structures in Mathematics and Physics (Roma 1999) (S. Marchiafava, P. Piccinni, M. Pontecorvo, eds) (World Scientific 2001), 23–30.CrossRefGoogle Scholar
A., Borel. Reduction theory for arithmetic groups. In “Algebraic Groups and Discontinuous Subgroups” (A. Borel and G. D. Mostow eds) Proc. Sympos. Pure Math. (Boulder, 1965) (Amer. Math. Soc. 1966), pp 20–25.Google Scholar
N., Bourbaki. Groupes et algÈbres de Lie : chap. 4, 5 et 6. (Masson, 1981).Google Scholar
E., Breuillard. Local limit theorems and equidistribution of random walks on the Heisenberg group. Geom. Funct. Anal. 15 (2005), 35–82.Google Scholar
A., Broise-Alamichel, J., Parkkonen and F., Paulin. Equidistribution and counting under equilibrium states in negative curvature and trees. Applications to non-Archimedean Diophantine approximation. With an Appendix by J. Buzzi. Progr. Math. 329 (Birkhäuser, 2019).CrossRefGoogle Scholar
F., Bruhat and J., Tits. Schémas en groupes et immeubles des groupes classiques sur un corps local. Bull. Soc. Math. France 112 (1984), 259–301.Google Scholar
F., Bruhat and J., Tits. Schémas en groupes et immeubles des groupes classiques sur un corps local. II : groupes unitaires. Bull. Soc. Math. France 115 (1987), 141–195.Google Scholar
W., Cao and J., Parker. JØ rgensen’s inequality and collars in n-dimensional quaternionic hyperbolic space. Quarterly J. Math. 62 (2011), 523–543.Google Scholar
W., Cao and J., Parker. Shimizu’s lemma for quaternionic hyperbolic space. Comput. Meth. Funct. Theo. 18 (2018), 159–191.Google Scholar
G., Chenevier and F., Paulin. Sur les minima des formes hamiltoniennes binaires définies positives. Publications Mathématiques de BesanÇon : AlgÈbre et théorie des nombres (2020), 5–25.CrossRefGoogle Scholar
K., Corlette. Hausdorff dimensions of limit sets I. Invent. Math. 102 (1990), 521–542.Google Scholar
M., Eichler. Über die Idealklassenzahl total definiter Quaternionenalgebren. Math. Z. 43 (1938), 102–109.Google Scholar
V., Emery. Du volume des quotients arithmétiques de l’espace hyperbolique. ThÈse n $^0$ 1648, Univ. Fribourg (Suisse) (2009).Google Scholar
V., Emery and I., Kim. Quaternionic hyperbolic lattices of minimal covolume. Preprint arXiv:1802.07776.Google Scholar
G. B., Folland and E. M., Stein. Estimates for the $\overline{\partial}_b$ complex and analysis on the Heisenberg group. Comm. Pure Appl. Math. 27 (1974), 429–522.Google Scholar
A., FrÖhlich. Locally free modules over arithmetic orders. J. reine angew. Math 274 (1975), 112–124.Google Scholar
W. M, Goldman. Complex Hyperbolic Geometry (Oxford University Press, 1999).Google Scholar
D., Gorenstein, R., Lyons and R., Solomon. The classification of the finite simple groups. Math. Surv. Mono. 40.1 (Amer. Math. Soc. 1994).CrossRefGoogle Scholar
M., Gromov and R., Schoen. Harmonic maps into singular spaces and p-adic superrigidity for lattices in groups of rank one. Publ. Math. IHéS 76 (1992), 165–246.Google Scholar
S., Helgason. Differential Geometry, Lie Groups and Symmetric Spaces (Academic Press, 1978).Google Scholar
I., Kim. Counting, mixing and equidistribution of horospheres in geometrically finite rank one locally symmetric manifolds. J. reine angew. Math. 704 (2015), 85–133.Google Scholar
I., Kim and J., Parker. Geometry of quaternionic hyperbolic manifolds. Math. Proc. Camb. Phil. Soc. 135 (2003), 291–320.Google Scholar
V., Krafft and D., Osenberg. Eisensteinreihen fÜr einige arithmetisch definierte Untergruppen von ${SL}_2({\mathbb{H}})$ . Math. Z. 204 (1990), 425–449.Google Scholar
S., Krantz. Explorations in harmonic analysis, with applications to complex function theory and the Heisenberg group. Appl. Num. Harm. Anal. (BirkhÄuser, 2009).CrossRefGoogle Scholar
G. D, Mostow. Strong rigidity of locally symmetric spaces. Ann. Math. Studies 78 (Princeton University Press, 1973).CrossRefGoogle Scholar
H., Oh and N., Shah. The asymptotic distribution of circles in the orbits of Kleinian groups. Invent. Math. 187 (2012), 1–35.Google Scholar
T., Ono. On algebraic groups and discontinuous groups. Nagoya Math. J. 27 (1966), 279–322.Google Scholar
J., Parkkonen and F., Paulin. Prescribing the behaviour of geodesics in negative curvature. Geom. Topo. 14 (2010), 277–392.Google Scholar
J., Parkkonen and F., Paulin. On the arithmetic and geometry of binary Hamiltonian forms. Appendix by Vincent Emery. Algebra & Number Theory 7 (2013), 75–115.Google Scholar
J., Parkkonen and F., Paulin. On the arithmetic of crossratios and generalised Mertens’ formulas. Special issue “Aux croisements de la géométrie hyperbolique et de l’arithmétique” (F. Dal’Bo, C. Lecuire eds) Ann. Fac. Sci. Toulouse 23 (2014), 967–1022.CrossRefGoogle Scholar
J., Parkkonen and F., Paulin. Skinning measure in negative curvature and equidistribution of equidistant submanifolds. Ergodic Theory Dynam. Systems 34 (2014), 1310–1342.Google Scholar
J., Parkkonen and F., Paulin. Counting common perpendicular arcs in negative curvature. Ergodic Theory Dynam. Systems 37 (2017), 900–938.Google Scholar
J., Parkkonen and F., Paulin. Counting and equidistribution in Heisenberg groups. Math. Annalen 367 (2017), 81–119.Google Scholar
J., Parkkonen and F., Paulin. Counting and equidistribution of quaternionic Cartan chains. Preprint arXiv:2002.05130, to appear in Ann. Math. Blaise Pascal.Google Scholar
Z., Philippe. Invariants globaux des variétés hyperboliques quaternioniques. Université de Bordeaux (Dec. 2016) https://tel.archives-ouvertes.fr/tel-01661448.Google Scholar
V, Platonov and A, Rapinchuck. Algebraic groups and number theory. Pure Appl. Math. 139 (Academic Press, 1994).Google Scholar
G., Prasad. Volumes of S-arithmetic quotients of semi-simple groups. Publ. Math. Inst. Hautes études Sci. 69 (1989), 91–117.Google Scholar
I., Reiner. Maximal Orders, (Academic Press, 1972).Google Scholar
T., Shemanske. The arithmetics and combinatorics of buidings for ${{Sp}}_n$ . Trans. Amer. Math. Soc 359 (2007), 3409–3423.Google Scholar
J., Tits. Classification of algebraic semisimple groups. In “Algebraic Groups and Discontinuous Subgroups” (Boulder, 1965) pp. 33–62. Proc. Symp. Pure Math. IX (Amer. Math. Soc. 1966).CrossRefGoogle Scholar
J., Tits. Reductive groups over local fields. In “Automorphic forms, representations and L-functions” (Corvallis, 1977), Part 1, pp. 29–69. Proc. Symp. Pure Math. XXXIII (Amer. Math. Soc., 1979).CrossRefGoogle Scholar
M. F., Vignéras. Arithmétique des algÈbres de quaternions. Lecture Notes in Math. 800 (Springer Verlag, 1980).CrossRefGoogle Scholar
T, Zink. Über die Anzahl der Spitzen einiger arithmetischer Untergruppen unitÄrer Gruppen. Math. Nachr. 89 (1979), 315–320.Google Scholar