Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Kastenbaum, Marvin A.
1966.
A dialysis system with one absorbing and one semi-reflecting state.
Journal of Applied Probability,
Vol. 3,
Issue. 2,
p.
365.
Kastenbaum, Marvin A.
1966.
A dialysis system with one absorbing and one semi-reflecting state.
Journal of Applied Probability,
Vol. 3,
Issue. 02,
p.
365.
Seneta, E.
1967.
ON THE MAXIMA OF ABSORBING MARKOV CHAINS.
Australian Journal of Statistics,
Vol. 9,
Issue. 3,
p.
93.
Sweet, Arnold L.
1980.
An Ad Hoc Method for Forecasting Series with Zero Values.
A I I E Transactions,
Vol. 12,
Issue. 1,
p.
97.
El-Shehawey, Mohamed A.
2008.
On Inverses of Tridiagonal Matrices Arising From Markov Chain-Random Walk I.
SIAM Journal on Matrix Analysis and Applications,
Vol. 30,
Issue. 2,
p.
497.

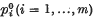 (
(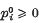 and
and 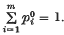 .
.