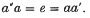1. Notation. For an arbitrary set X, |X| will denote its cardinal number. Rn and Tn will denote the n-dimensional real vector space and the n-dimensional torus respectively with the usual topologies.

A graph consists of a finite set of points and a set of lines joining some pairs of these points. At most one line is permitted to join any two points and no point is joined to itself by a line. A graph G′ is a subgraph of the graph G if the points and lines of G′ are also points and lines of G. The union of several graphs having the same set of points is the graph formed by joining two points in this set if they are joined in at least one of the original graphs. A graph is planar if it can be drawn in the plane (or equivalently, on a sphere) so that no lines intersect. The thickness of a graph G is defined as the smallest integer t such that G is the union of t planar subgraphs.

1. The notation used will be that of (2).

G is a finite group,

is a ring which is either

(1·1) a field of characteristic p, or

(1·2) the ring of valuation integers of a field of characteristic 0 with a complete discrete valuation. In this case, is the maximal ideal of .

Solutions for the temperature distribution in a circular pipe have been given by various authors, notably Gretz, Nusselt, Goldstein; all these are cited in (1), section 266. I have already considered in one paper the temperature distribution in a circular pipe when viscous incompressible fluid is flowing through the pipe and rate of heat addition is an oscillatory function of time. In this paper expressions for the temperature distributions are derived when viscous incompressible fluid is flowing through the channel, the dissipation due to friction is neglected and the rate of heat addition is an exponential function of time. From the engineering point of view this situation has some importance.

Introduction. This paper falls into three parts.

In §§ 1–5 it is explained how, when the base field of the geometry is GF(2), there are figures of n + 2 interlocking polygons in [n], every two polygons sharing a vertex. When n is even these ½(n + 1) (n + 2) vertices lie in an [n − 1], and two of them are conjugate in a certain null polarity when, and only when, they do not belong to the same polygon.

1. In this paper we wish to discuss some problems which arise from a paper by Lorentz and Zeller; see (5). If {μn} is a fixed sequence monotonically increasing to infinity, and every sequence {sn} summed by both of the regular matrices A = (amn) and B = (bmn) and satisfying sn = O{μn) is summed to the same value by both matrices, the matrices are called (μn)-consistent. The two matrices are called consistent if they are (μn)-consistent for all {μn}, μn↗∞; they are b-consistent if the bounded sequences summed by both are summed to the same value by both. The matrix A is said to be (μn)-stronger than the matrix B, if every sequence {μn} that is B summable and satisfying sn = O(μn) is also A summable. The matrix A is stronger than B if every B summable sequence is A summable; A is b-stronger if every bounded B summable sequence is A summable. The symbol A -lim x denotes the value to which the sequence x = {xn} is summed by A; Am(x) is the transformation

and A(x) is the sequence {Am(x)}. Let {A(i)}i ∈ I be any family, infinite or finite, of regular summability matrices. This family is called simultaneously consistent if, given any finite subset of I, say F, and any set of sequences {x(i)i ∈ F such that A(i) sums x(i) for each i in F, and such that is the null sequence, then .

In this paper we consider the problem of dividing a square of side N into squares of integral side. When we demand that these be unequal, the problem is soluble only for certain N, and has been treated in some detail by various authors (1,3,4,5). If we relax this condition, every side is permissible, for a square of side N may plainly be divided into N2 squares of side 1. It is the object of this paper to reduce this number: in fact we shall show that a square of side N is divisible into some number less than 6 ∛N + 1 squares of integral side.

1. Introduction. In (7), a theory was developed which dealt with certain classes of partial algebras in which the domains of the operators were determined by an ‘operator scheme’. This device allows the use of methods normally available only for full abstract algebras. In particular, one can present suitable partial algebras by means of generators and relations.

1. Introduction. The open subsets of a topological space X form a complete Brouwerian, i.e. distributive and pseudo-complemented lattice L(X). Many topological properties of X can be formulated as properties of L(X), although, in general, X is not determined by L(X). Obvious examples are quasi-compactness and connectivity: X is quasi-compact if any set of elements of L(X) whose join is I has a finite subset whose join is I; X is connected if no element of L(X) has a complement. These properties which we shall call ‘paratopological’, can be defined for lattices that are not of the form L(X), and many topological theorems can be proved in this more general context. The purpose of this paper is to develop sections of general topology as part of the theory of complete Brouwerian lattices (CBL).

In (2) we defined the Künneth suspension of a cohomology operation —the Künneth suspension involves an arbitrary css-complex Y rather than the 1-sphere S1, as with the usual suspension of a cohomology operation. Now the suspension homomorphism is well known to be related to the operation of forming loop spaces (cf. (4)). The main object of this paper is to prove a similar result for the Künneth suspension.

A set Q is quasi-ordered if a reflexive and transitive relation ≤ is defined on Q. It is well-quasi-ordered if it is quasi-ordered and, for every infinite sequence u1, u2,… of elements of Q, there exist i, j such that i < j and ui ≤ uj. A lower set of Q is a subset P of Q such that, if x ≤ y ∈ P, then x ∈ P. The class of lower sets of Q, quasi-ordered by ⊂, is denoted by LQ, and L2Q = L(LQ), etc. The set (, say) of all finite trees is quasi-ordered by writing T1 ≤ T2 if T1 is homeomorphic to a subtree of T2. It is proved that is well-quasi-ordered for all n.

A group is said to have the property T or to be a T-group if every subnormal subgroup is normal. Thus the class of T-groups is just the class of all groups in which normality is a transitive relation. Finite T-groups have been studied by Best and Taussky (l), Gaschütz (4) and Zacher (11). Gaschütz has shown that if G is a finite soluble T-group and G/L is the unique maximal nilpotent quotient group of G, then G/L is Abelian or Hamiltonian and L is an Abelian group of odd order prime to |G:L| ((4), Satz 1). Our aim is to study infinite T-groups and more especially infinite soluble T-groups with a view to extending Gaschütz's results. One of the simplest results on soluble T-groups is THEOREM 2.3.1. Every soluble T-group is metabelian.

1. Objective. It is possible to define order convergence on the vector lattice of all continuous functions of compact support on a locally compact topological space. Every measure is a linear form on this vector lattice. The object of this paper is to prove that a measure is such that every set of the first category of Baire has measure zero if and only if the measure is a linear form which is continuous in the order convergence.

There is a sense in which the homology group HA of a free Abelian chain complex A may be said to be a ‘complete system of invariants’ of A, to within chain equivalence; certainly any graded Abelian group G is isomorphic to HA for a suitable A, and if HA and HB are isomorphic then A and B are chain equivalent. Such a result is useful in showing that it is fruitless to seek other homotopy invariants of A; whatever depends only on the homotopy class of A depends only on HA, so that we can, for instance, predict the existence of a formula giving H(A ⊗ G), to within isomorphism, in terms of HA and G. The theorem on the existence and uniqueness to within chain equivalence of projective resolutions of modules is a variant of the above theorem, more general in one direction and more special in another.

It is well known that, with respect to the natural partial ordering, the set of all congruences on a group forms a modular lattice. In the present paper we develop an extension of this result to the case of a regular semigroup S (α ∈ αSα for all α in S). Let Σ(ℋ) denote the set of all congruences on S with the property that congruent elements generate the same principal left ideal and the same principal right ideal of S. We show (Theorem 1) that, under the natural partial ordering, Σ(ℋ) is a modular lattice with a greatest and a least element.

The absolute simplicial approximation theorem, which dates back to Alexander (l), states that there is a simplicial approximation g to any given continuous map f between two finite simplicial complexes (see for instance (2), p. 37 or (3), p. 86). The relative theorem given here permits us to leave f unchanged on any subcomplex, on which f happens to be already simplicial.

1. Introduction. Consider a set P with elements a, b, c,… and a certain distinguished element e. Assume that P satisfies the following conditions.

(I) With each ordered pair (a, b) of distinct elements a and b of P there is associated a unique element of P (to be denoted by ab and called the product of a and b). Further, with the pair (e, e) there is associated a unique element ee of P.

(II)(ab)c = a(bc) for all elements a, b, c in P for which both sides are defined.

(III) ea = a = ae for all elements a ∈ P.

(IV) To each element a ∈ P, there corresponds an element a′ ∈ P such that

1. Let {Vi}i≥0 be a weakly (hence also strongly) continuous semigroup of (linear) contraction operators on a Hilbert space H, i.e. |Vt| ≤ 1 ( t ≥ 0). Let Z and W denote the corresponding infinitesimal generator and cogenerator, i.e.

Z is in general non-bounded, but closed and densely defined, and W is a contraction operator (everywhere defined in H), such that 1 is not a proper value of W. Conversely, every contraction operator W not having the proper value 1 is the infinitesimal cogenerator of exactly one semigroup {Vi} of the above type; one has namely

in the sense of the functional calculus for contraction operators (4).

The irregular radial Coulomb wave function is expanded in a convergent series of Bessel functions in which the coefficients are expressed in powers of the energy and the argument of the Bessel functions depends on the radius only and not on the energy. This formulation is suitable for low-energy particles. The corresponding expansion for the regular Coulomb function can be deduced from previous work by Tricomi.

This is the second paper of a series, and supposes familiarity with the results and the notations of the first(l), which we refer to as I.