No CrossRef data available.
Article contents
Images of fractional Brownian motion with deterministic drift: Positive Lebesgue measure and non-empty interior
Published online by Cambridge University Press: 28 February 2022
Abstract
Let
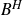 $B^{H}$
be a fractional Brownian motion in
$B^{H}$
be a fractional Brownian motion in
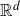 $\mathbb{R}^{d}$
of Hurst index
$\mathbb{R}^{d}$
of Hurst index
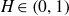 $H\in\left(0,1\right)$
,
$H\in\left(0,1\right)$
,
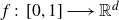 $f\;:\;\left[0,1\right]\longrightarrow\mathbb{R}^{d}$
a Borel function and
$f\;:\;\left[0,1\right]\longrightarrow\mathbb{R}^{d}$
a Borel function and
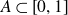 $A\subset\left[0,1\right]$
a Borel set. We provide sufficient conditions for the image
$A\subset\left[0,1\right]$
a Borel set. We provide sufficient conditions for the image
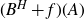 $(B^{H}+f)(A)$
to have a positive Lebesgue measure or to have a non-empty interior. This is done through the study of the properties of the density of the occupation measure of
$(B^{H}+f)(A)$
to have a positive Lebesgue measure or to have a non-empty interior. This is done through the study of the properties of the density of the occupation measure of
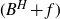 $(B^{H}+f)$
. Precisely, we prove that if the parabolic Hausdorff dimension of the graph of f is greater than Hd, then the density is a square integrable function. If, on the other hand, the Hausdorff dimension of A is greater than Hd, then it even admits a continuous version. This allows us to establish the result already cited.
$(B^{H}+f)$
. Precisely, we prove that if the parabolic Hausdorff dimension of the graph of f is greater than Hd, then the density is a square integrable function. If, on the other hand, the Hausdorff dimension of A is greater than Hd, then it even admits a continuous version. This allows us to establish the result already cited.
MSC classification
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 173 , Issue 3 , November 2022 , pp. 693 - 713
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society


