No CrossRef data available.
Links with super-additive tunnel number
Published online by Cambridge University Press: 24 October 2008
Extract
Let L ⊂ S3 be a knot or a link. A tunnel system for L is a collection of disjoint arcs t1, … ts properly embedded in S3−N(L) so that 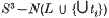 is a handlebody. Alternatively one can view the t1, … ts ascocores of 2-handles which have to be attached to a handlebody in order to obtain S3−N(L). It follows immediately that this handlebody is of genus s+1. The tunnel number of L, denoted by t(L), is defined to be the minimal cardinality of all such collections.
is a handlebody. Alternatively one can view the t1, … ts ascocores of 2-handles which have to be attached to a handlebody in order to obtain S3−N(L). It follows immediately that this handlebody is of genus s+1. The tunnel number of L, denoted by t(L), is defined to be the minimal cardinality of all such collections.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 115 , Issue 1 , January 1994 , pp. 85 - 95
- Copyright
- Copyright © Cambridge Philosophical Society 1994
References
REFERENCES
[1]Birman, J. and Hilden, H.. The homeomorphism problem for S 3. Bull. Amer. Math. Soc. 79 (1973), 1006–1010.CrossRefGoogle Scholar
[2]Doll, H.. Generalized bridge number for links in 3-manifolds, preprint 1991.CrossRefGoogle Scholar
[3]Gonzáles-Acuñna, F. and Short, H.. Knot surgery and primeness. Math. Proc. Cambridge Philos. Soc. 99 (1986), 89–102.CrossRefGoogle Scholar
[4]Jaco, W.. Lectures on three-manifold topology. Regional conf. series in math. 43, A.M.S. 1980.CrossRefGoogle Scholar
[5]Lustig, M.. On the Rank, the Deficiency and the Hcmological Dimension of Groups: The Computation of a Lower Bound via Fox Ideals, in Topology and Combinatorial Group Theory, Latiolais, P. (ed.), Lecture Notes in Mathematics 1440, 164–174. (Springer Verlag, 1991.)Google Scholar
[6]Lustig, M. and Moriah, Y.. Generating Systems for Groups and Reidemeister–Whitehead Torsion, to appear in J. of Algebra.Google Scholar
[7]Lustig, M. and Moriah, Y.. Generalized Montesinos Knots, Tunnels and N-Torsion, to appear in Math. Annalen.Google Scholar
[8]Montesinos, J.. Surgery on links and double branched coverings of S 3, in Knots, Groups, and 3-Manifolds, Neurwith, L. P. (ed.), Annals of Math. Studies 84 227–260 (Princeton University Press 1975).CrossRefGoogle Scholar
[9]Morimoto, K.. On behavior of tunnel number of knots under connected sum, preprint 1992.Google Scholar
[10]Norwood, F.. Every two-generator knot is prime. Proc. A.M.S. 86 (1982), 143–147.CrossRefGoogle Scholar
[11]Viro, O.. Linkings, 2-sheeted branched coverings and braids. Math. USSR Sbornik 16 (1972), 223–226.CrossRefGoogle Scholar


