Research Article
Curves with increasing chords
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-12
-
- Article
- Export citation
Reflections in extended Bianchi groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 13-25
-
- Article
- Export citation
Locating the radical of a triangular operator algebra
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 27-38
-
- Article
- Export citation
Minimal primal ideals in Banach algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 39-52
-
- Article
- Export citation
Skeins and mapping class groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 53-77
-
- Article
- Export citation
On the cofiniteness of local cohomology modules
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 79-84
-
- Article
- Export citation
Links with super-additive tunnel number
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 85-95
-
- Article
- Export citation
Covering groups of non-connected topological groups revisited
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 97-110
-
- Article
- Export citation
Remarks on structurally stable proper foliations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 111-120
-
- Article
- Export citation
Lefschetz numbers of periodic orbits of pseudo-Anosov homeomorphisms
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 121-132
-
- Article
- Export citation
Spaces of operators between Fréchet spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 133-144
-
- Article
- Export citation
Ω theorems for the complex divisor function
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 145-157
-
- Article
- Export citation
Poincaré and Friedrichs inequalities in abstract Sobolev spaces II
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 159-173
-
- Article
- Export citation
Maximal inequalities of Kahane–Khintchine's type in Orlicz spaces
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 175-190
-
- Article
- Export citation
Front matter
PSP volume 115 issue 1 Cover and Front matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back matter
PSP volume 115 issue 1 Cover and Back matter
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. b1-b2
-
- Article
-
- You have access
- Export citation

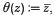 , adjoined. (
, adjoined. (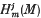 are artinian,
are artinian, 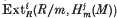 is finitely generated for all
is finitely generated for all 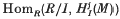
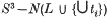 is a handlebody. Alternatively one can view the
is a handlebody. Alternatively one can view the 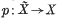 be the universal cover of the underlying space of
be the universal cover of the underlying space of 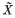 with
with 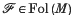 ∈ Fol(
∈ Fol(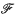 in Fol(
in Fol(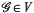 is topologically conjugate to
is topologically conjugate to 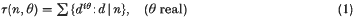
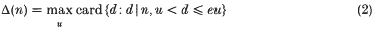

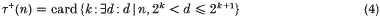
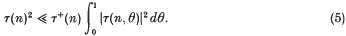
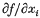 belongs to Y; equipped with the norm
belongs to Y; equipped with the norm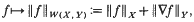
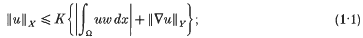
 in
in 
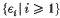 is a Bernoulli sequence, and ‖ · ‖
is a Bernoulli sequence, and ‖ · ‖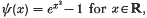 then the following inequality is satisfied:
then the following inequality is satisfied: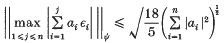
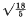 lies in the interval ]
lies in the interval ]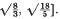 . Sharp estimates of this type are also deduced for some other maximal inequalities in Orlicz spaces discovered in this paper.
. Sharp estimates of this type are also deduced for some other maximal inequalities in Orlicz spaces discovered in this paper.