Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-28T01:38:23.868Z Has data issue: false hasContentIssue false
  • English
  • Français

On dichotomy of Riesz products

Published online by Cambridge University Press:  24 October 2008

G. Ritter
G. Ritter
Affiliation:
(Mathematisches Institut, Erlangen, Federal Republic of Germany and University of Washington, Seattle)
Get access Rights & Permissions [Opens in a new window]

Extract

Background. Riesz products are very useful for the construction of singular measures on compact, Abelian groups. Under some circumstances, two Riesz products are either equivalent or singular in the measure-theoretic sense. Exact knowledge of these circumstances has been of major interest ever since the 1930s, when Riesz's famous example (8) was recognized as a fertile source of examples of singular continuous measures. Zygmund(11) showed that any Riesz product over a Hadamard dissociate subset of ℕ is either a square integrable function or singular with respect to Lebesgue measure. Hewitt–Zuckerman(4) generalized these products to all compact, Abelian groups, introducing the notion of a dissociate subset. They extended Zygmund's result in certain cases. The next major step was taken by Brown–Moran(3) and Peyrière(6), (7), who showed that two Riesz products

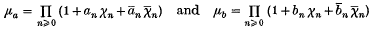
are mutually singular if

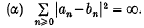
The author (9) has improved another result of Brown–Moran (3) by showing that µa and µb are equivalent if

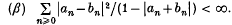
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 85 , Issue 1 , January 1979 , pp. 79 - 89
Copyright
Copyright © Cambridge Philosophical Society 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Brown, G.Riesz products and generalized characters. Proc. London Math. Soc. 30 (1975), 209–238.CrossRefGoogle Scholar
(2)Brown, G. and Moran, W.A dichotomy for infinite convolutions of discrete measures. Proc. Cambridge Philos. Soc. 73 (1973), 307–316.CrossRefGoogle Scholar
(3)Brown, G. and Moran, W.On orthogonality of Riesz products. Proc. Cambridge Philos. Soc. 76 (1974), 173–181.CrossRefGoogle Scholar
(4)Hewitt, E. and Zuckerman, H. S.Singular measures with absolutely continuous convolution squares. Proc. Cambridge Philos. Soc. 62 (1966), 399–420.CrossRefGoogle Scholar
(4)Hewitt, E. and Zuckerman, H. S.Singular measures with absolutely continuous convolution squares. Proc. Cambridge Philos. Soc.Google Scholar
Corrigendum, Hewitt, E. and Zuckerman, H. S.Singular measures with absolutely continuous convolution squares. Proc. Cambridge Philos. Soc. 63 (1967), 367–368.CrossRefGoogle Scholar
(5)Kakutani, S.On equivalence of infinite product measures. Ann. of Math. 49 (1948), 214–224.CrossRefGoogle Scholar
(6)Peyrière, J.Sur les produits de Riesz. C.R. Acad. Sci., Paris 276 (1973), 1417–1419.Google Scholar
(7)Peyrière, J.Etude de quelques propriétés des produits de Riesz. Ann. Inst. Fourier 25 2 (1975), 127–169.CrossRefGoogle Scholar
(8)Riesz, F.Über die Fourierkoeffizienten einer stetigen Funktion von beschränkter Schwankung. Math. Z. 2 (1918), 312–315.CrossRefGoogle Scholar
(9)Ritter, G.Unendliche Produkte unkorrelierter Funktionen auf kompakten, abelschen Gruppen. Math. Scand. 42 (1978) (in the Press).CrossRefGoogle Scholar
(10)Ritter, G.On Kakutani's dichotomy theorem for infinite products of not necessarily independent functions. Math. Ann. (in the Press).Google Scholar
(11)Zygmund, A.On lacunary trigonometric series. Trans. Amer. Math. Soc. 34 (1932), 435–446.CrossRefGoogle Scholar