Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T05:56:17.100Z Has data issue: false hasContentIssue false
  • English
  • Français

The vorticity equation as an angular momentum equation

Published online by Cambridge University Press:  24 October 2008

P. C. Chatwin
P. C. Chatwin
Affiliation:
Department of Applied Mathematics, The University of Liverpool
Get access Rights & Permissions [Opens in a new window]

Extract

In a Newtonian fluid, in which the body forces are conservative, in which the pressure is a function only of density and in which the kinematic viscosity v is uniform, the vorticity ω satisfies the equation

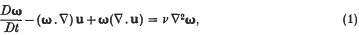
where u is the velocity field, so that ω = ▿ × u. This equation is normally derived by taking the curl of the Navier–Stokes equations. However, the vorticity has many interpretations in terms of the angular velocity of elements of fluid and it is natural to expect that (1) can be derived by equating the rate of change of the angular momentum of a small material volume element about its centre of mass with the moment of the forces acting on the element. Such a derivation is presented here in the hope that it may be of pedagogic interest.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 74 , Issue 2 , September 1973 , pp. 365 - 367
Copyright
Copyright © Cambridge Philosophical Society 1973

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

(1)Batchelor, G. K.An introduction to fluid dynamics (Cambridge University Press, 1967).Google Scholar