Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-14T22:07:42.014Z Has data issue: false hasContentIssue false
  • English
  • Français

The action in a uniform field

Published online by Cambridge University Press:  24 October 2008

L. A. Pars
L. A. Pars
Affiliation:
Jesus CollegeCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

We consider the motion of a particle in a plane field of force. We take rectangular cartesian coordinates (x, y) in the plane, and denote by V(x, y) the potential of the field, and by h the (constant) energy of the motion. If A and B, whose coordinates are (x0, y0) and (x1, y1), are any two points on an orbit, the orbit is characterized by the property that

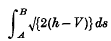
taken along the orbit is stationary as compared with the integral taken along a neighbouring curve joining the same points. Here s denotes the length of the are measured from A to B. This is one form, sometimes called Jacobi's form, of the principle of least action. The value of the integral, taken along the orbit, and expressed in terms of the coordinates of the termini and the constant of energy,

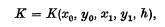
is the action function for the field V.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 37 , Issue 2 , April 1941 , pp. 168 - 176
Copyright
Copyright © Cambridge Philosophical Society 1941

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

* Bolza, O., Vorlesungen über Variationsrechnung (1933), p. 80.Google Scholar

* Bolza, ibid. p. 123.

* The formula for K was evaluated, by a different method from that given above, by Darboux, , Théorie Générale des Surfaces, 2 (1889), p. 448.Google Scholar

* Bolza, ibid. p. 398.

* Bolza, ibid. pp. 436–8.

† Todhunter, I., Researches in the calculus of variations (1871), p. 60.Google Scholar