No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Let S0 be a complex projective surface with only isolated Gorenstein singularities (see Introduction to (12)). By Serre's criterion ((4), p. 185) this is equivalent to saying that S0 is normal and Gorenstein. By an algebraic smooth deformation of S0, we shall mean a flat, proper morphism of varieties, ρ: 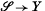 say, with fibre ρ−1(y0) = S0 for some y0 ∈ Y and with the general fibre ρ−1(y) = S being a smooth surface. In the paper (12), we studied such smooth deformations of S0 and in particular the behaviour of the plurigenera Pn of the surfaces in the family. The main result of (12) was the fact that Pn(S0) ≤ Pn(S) for all positive integers n, where the choice of the particular smooth surface was irrelevant by a result of Iitaka(5). To prove the above result we introduced what were called the arithmetic plurigenera of S0, which we define again below. In this paper we shall study more closely these arithmetic quantities, and in the process answer some of the questions posed in (11).
say, with fibre ρ−1(y0) = S0 for some y0 ∈ Y and with the general fibre ρ−1(y) = S being a smooth surface. In the paper (12), we studied such smooth deformations of S0 and in particular the behaviour of the plurigenera Pn of the surfaces in the family. The main result of (12) was the fact that Pn(S0) ≤ Pn(S) for all positive integers n, where the choice of the particular smooth surface was irrelevant by a result of Iitaka(5). To prove the above result we introduced what were called the arithmetic plurigenera of S0, which we define again below. In this paper we shall study more closely these arithmetic quantities, and in the process answer some of the questions posed in (11).