Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-14T22:05:34.677Z Has data issue: false hasContentIssue false
  • English
  • Français

Augmentation quotients of group rings and symmetric powers

Published online by Cambridge University Press:  24 October 2008

Robert Sandling  and
Ken-Ichi Tahara
Robert Sandling
Affiliation:
The University, Manchester, M13 9PL, England
Ken-Ichi Tahara
Affiliation:
Aichi University of Education, Igaya-cho, Kariya-shi, 448, Japan
Get access Rights & Permissions [Opens in a new window]

Extract

Let G be a group with the lower central series

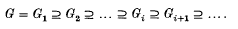
Let

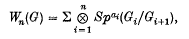
where Σ runs over all non-negative integers a1, a2,…, an such that 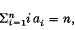and 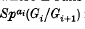is the aith symmetric power of the abelian group Gi/Gi+1 where

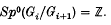
Let I (G) be the augmentation ideal of G in 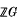, the group ring of G over 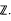. Define the additive group Qn (G) = In (G) / In+1 (G) for any n ≥ 1. Then it is well known that Q1(G) ≅ W1(G) for any group G. Losey (4,5) proved that Q2(G) ≅ W2(G) for any finitely generated group G. Furthermore recently Tahara(12) proved that Q3(G) is a certain precisely defined quotient of W3(G) for any finite group G.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 85 , Issue 2 , March 1979 , pp. 247 - 252
Copyright
Copyright © Cambridge Philosophical Society 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Grün, O.Über eine Faktorgruppe freier Gruppen, I. Deutsche Math. 1 (1936), 772–782.Google Scholar
(2)Hall, P.Nilpotent groups. Canad. Math. Congress, Univ. of Alberta, 1957; Queen Mary College Math. Notes, 1969.Google Scholar
(3)Hartley, B.The residual nilpotence of wreath products. Proc. London Math. Soc. (3) 20 (1970), 365–392.Google Scholar
(4)Losey, G.On the structure of Q 2(G) for finitely generated groups. Canad. J. Math. 25 (1973), 353–359.CrossRefGoogle Scholar
(5)Losey, G.N-series and filtrations of the augmentation ideal. Canad. J. Math. 26 (1974), 962–977.Google Scholar
(6)MaCmahon, P. A.Combinatory analysis, vol. I (Cambridge, Cambridge University Press, 1915).Google Scholar
(7)Magnus, W.¨Uber Beziehungen zwischen höheren Kommutatoren. J. Reine Angew. Math. 177 (1937), 105–115.CrossRefGoogle Scholar
(8)Passi, I. B. S.Polynomial maps on groups. J. Algebra 9 (1968), 121–151.CrossRefGoogle Scholar
(9)Passi, I. B. S.Polynomial functors. Proc. Cambridge Philos. Soc. 66 (1969), 505–512.Google Scholar
(10)Quillen, D. G.On the associated graded ring of a group ring. J. Algebra 10 (1968), 411–418.CrossRefGoogle Scholar
(11)Sandling, R.Dimension subgroups over arbitrary coefficient rings. J. Algebra 21 (1972), 250–265.CrossRefGoogle Scholar
(12)Tahara, K.On the structure of Q 3(G) and the fourth dimension subgroups. Japan. J. Math. (N.S.) 3 (1977), 381–394.Google Scholar
(13)Tahara, K. The augmentation quotients of group rings and the fifth dimension subgroups. (To appear).Google Scholar