Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-14T22:39:49.977Z Has data issue: false hasContentIssue false
  • English
  • Français

Bounded-weak topologies and completeness in vector spaces

Published online by Cambridge University Press:  24 October 2008

G. T. Roberts
G. T. Roberts
Affiliation:
King's CollegeCambridge
Get access Rights & Permissions [Opens in a new window]

Extract

Suppose that X is any vector space on which it is possible to recognize a class of sets of such a nature that it is natural to call them ‘bounded’. (Precise conditions for such a class of sets are given in § 2.) Let L be any vector space of linear functionals on X which map each ‘bounded’ set into a bounded set. We say that a filter 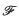is boundedly-weakly convergent if it is convergent in the weak topology of the linear system [X, L] and contains a ‘bounded’ set. If M is a vector space of boundedly-weakly continuous linear functionals on X which includes L, we say that a subset S of M is limited if 〈 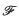, f〉 converges uniformly for f ε S whenever 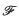is a boundedly-weakly convergent filter.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 49 , Issue 2 , April 1953 , pp. 183 - 189
Copyright
Copyright © Cambridge Philosophical Society 1953

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Arens, R.Duke math. J. 14 (1947), 787–94.Google Scholar
(2)Bourgin, D. C.Amer. J. Math. 65 (1943), 637–59.CrossRefGoogle Scholar
(3)Dieudonné, J.Proc. Amer. math. Soc. 1 (1950), 54–9.CrossRefGoogle Scholar
(4)Dieudonné, J. and Schwartz, L.Ann. Inst. Fourier, 1 (1949), 61–101.CrossRefGoogle Scholar
(5)Grothendieck, A.C.R. Acad. Sci., Paris, 230 (1950), 605–6.Google Scholar
(6)Koethe, G.Math. Nachr. 4 (1950), 70–80.Google Scholar
(7)Mackey, G. W.Trans. Amer. math. Soc. 57 (1945), 155–207.CrossRefGoogle Scholar