Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-27T08:50:43.415Z Has data issue: false hasContentIssue false
  • English
  • Français

Concerning automorphisms in finitely generated Abelian groups

Published online by Cambridge University Press:  24 October 2008

H. Liebeck
H. Liebeck
Affiliation:
Department of Mathematics, University of Keele, Staffordshire
Get access Rights & Permissions [Opens in a new window]

Extract

Of particular importance in the structure theory of finitely generated groups are those groups G having the property ℳd that for any two sets of generators g1, …, gd; h1, …, hd of G there is an automorphism θ of G such that 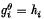(i = 1, …, d). Gaschütz(1) proved that all groups G having† ℳd also possess a further manifestation of symmetry, the property that if M and N are finite normal subgroups of G, any isomorphism between G/M and G/N can be induced by an automorphism of G. The case in which G is a finite p-group had previously been considered by Taunt (6) and Liebeck(2), who proved that for such groups the above property on the quotient groups of G is equivalent to ℳd.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 59 , Issue 1 , January 1963 , pp. 25 - 31
Copyright
Copyright © Cambridge Philosophical Society 1963

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Gaschütz, W.Zu einem von, B. H. und Neumann, H. gestellten Problem. Math. Nachr. 14 (1956), 249–252.CrossRefGoogle Scholar
(2)Liebeck, H.A note on prime-power groups with symmetrical generating relations. Proc. Cambridge Philos. Soc. 51 (1955), 394–395.CrossRefGoogle Scholar
(3)Neumann, B. H. and Neumann, H.Zwei Klassen charakteristischer Untergruppen und ihre Faktorgruppen. Math. Nachr. 4 (1951), 106–125.Google Scholar
(4)Neumann, B. H.On a question of Gaschütz. Arch. Math. 7 (1956), 87–90.CrossRefGoogle Scholar
(5)Shoda, K.Über die Automorphismen einer endlichen Abelschen Gruppe. Math. Ann. 100 (1928), 674–686.CrossRefGoogle Scholar
(6)Taunt, D. R.Remarks on the isomorphism problem in theories of construction of finite groups. Proc. Cambridge Philos. Soc. 51 (1955), 16–24.CrossRefGoogle Scholar