Research Article
Coset enumeration on digital computers
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 257-267
-
- Article
- Export citation
Cubic forms over algebraic number fields
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 683-705
-
- Article
- Export citation
A second note on the simple group of order 6048
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 1-9
-
- Article
- Export citation
On the representation and enumeration of trees
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 509-517
-
- Article
- Export citation
Generalized Gâteaux and Fréchet derivatives in convolution algebras
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 707-718
-
- Article
- Export citation
On a conjecture of Barnes and Swinnerton-Dyer
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 519-522
-
- Article
- Export citation
The Wiener–Pitt phenomenon on semi-groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 11-24
-
- Article
- Export citation
A note on the coefficients of Hilbert characteristic functions in semi-regular local rings
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 269-275
-
- Article
- Export citation
A topological proof in group theory
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 277-282
-
- Article
- Export citation
The volume of a lattice polyhedron
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 719-726
-
- Article
- Export citation
Concerning automorphisms in finitely generated Abelian groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 25-31
-
- Article
- Export citation
The minimization of a general function subject to a set of non-linear constraints
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 523-530
-
- Article
- Export citation
On non-strictly simple groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 531-553
-
- Article
- Export citation
A note on normal operators
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 727-729
-
- Article
- Export citation
A note on natural maps of higher extension functors
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 283-286
-
- Article
- Export citation
On a problem of Erdős concerning decompositions of the plane
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 33-36
-
- Article
- Export citation
On the Steinhaus billiard table problem
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 37-41
-
- Article
- Export citation
Note on the reduction of dual and triple series equations to dual and triple integral equations
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 731-734
-
- Article
- Export citation
Gradient configurations and quadratic functions
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 287-305
-
- Article
- Export citation
Packings, free products and residually finite groups
-
- Published online by Cambridge University Press:
- 24 October 2008, pp. 555-558
-
- Article
- Export citation

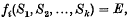
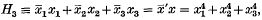
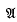 be a commutative normed algebra whose elements are functions on a Banach space, and in which the product is of convolution type. We show how
be a commutative normed algebra whose elements are functions on a Banach space, and in which the product is of convolution type. We show how  contains mean Gâteaux or Fréchet differentials of all its members. In this way the function algebra
contains mean Gâteaux or Fréchet differentials of all its members. In this way the function algebra 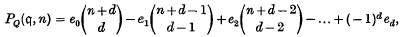
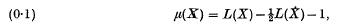
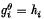 (
( that if
that if 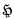 is said to be
is said to be 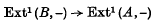
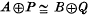 . One can ask whether these theorems remain true for higher extension functors.
. One can ask whether these theorems remain true for higher extension functors. be a plane closed convex curve, and regard
be a plane closed convex curve, and regard