Published online by Cambridge University Press: 09 July 2021
We study the integrability of the conformal geodesic flow (also known as the conformal circle flow) on the SO(3)–invariant gravitational instantons. On a hyper–Kähler four–manifold the conformal geodesic equations reduce to geodesic equations of a charged particle moving in a constant self–dual magnetic field. In the case of the anti–self–dual Taub NUT instanton we integrate these equations completely by separating the Hamilton–Jacobi equations, and finding a commuting set of first integrals. This gives the first example of an integrable conformal geodesic flow on a four–manifold which is not a symmetric space. In the case of the Eguchi–Hanson we find all conformal geodesics which lie on the three–dimensional orbits of the isometry group. In the non–hyper–Kähler case of the Fubini–Study metric on 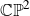 $\mathbb{CP}^2$ we use the first integrals arising from the conformal Killing–Yano tensors to recover the known complete integrability of conformal geodesics.
$\mathbb{CP}^2$ we use the first integrals arising from the conformal Killing–Yano tensors to recover the known complete integrability of conformal geodesics.