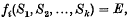Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Mendelsohn, N. S.
1964.
An Algorithmic Solution for a Word Problem in Group Theory.
Canadian Journal of Mathematics,
Vol. 16,
Issue. ,
p.
509.
Trotter, H. F.
1964.
A Machine Program for Coset Enumeration.
Canadian Mathematical Bulletin,
Vol. 7,
Issue. 3,
p.
357.
Leech, John
1965.
Generators for certain normal subgroups of (2,3,7).
Mathematical Proceedings of the Cambridge Philosophical Society,
Vol. 61,
Issue. 2,
p.
321.
Cannon, John J.
1969.
Computers in group theory.
Communications of the ACM,
Vol. 12,
Issue. 1,
p.
3.
NEUBÜSER, J.
1970.
Computational Problems in Abstract Algebra.
p.
1.
LEECH, JOHN
1970.
Computational Problems in Abstract Algebra.
p.
21.
Dimino, Lucien A.
1971.
A graphical approach to coset enumeration.
ACM SIGSAM Bulletin,
p.
8.
1971.
Elements of Combinatorial Computing.
p.
243.
Cannon, John J.
Dimino, Lucien A.
Havas, George
and
Watson, Jane M.
1973.
Implementation and analysis of the Todd-Coxeter algorithm.
Mathematics of Computation,
Vol. 27,
Issue. 123,
p.
463.
Macdonald, I.D.
1973.
Computer results on Burnside groups.
Bulletin of the Australian Mathematical Society,
Vol. 9,
Issue. 3,
p.
433.
Cannon, John J.
1973.
Construction of defining relators for finite groups.
Discrete Mathematics,
Vol. 5,
Issue. 2,
p.
105.
Macdonald, I. D.
1974.
A computer application to finite p-groups.
Journal of the Australian Mathematical Society,
Vol. 17,
Issue. 1,
p.
102.
Newman, M.F.
1976.
A computer aided study of a group defined by fourth powers.
Bulletin of the Australian Mathematical Society,
Vol. 14,
Issue. 2,
p.
293.
McLain, D. H.
1977.
An algorithm for determining defining relations of a subgroup.
Glasgow Mathematical Journal,
Vol. 18,
Issue. 1,
p.
51.
Jura, Andrzej
1978.
Coset Enumeration in a Finitely Presented Semigroup.
Canadian Mathematical Bulletin,
Vol. 21,
Issue. 1,
p.
37.
Jürgensen, H.
1979.
Transformationendarstellungen endlicher abstrakt präsentierter Halbgruppen.
Computing,
Vol. 21,
Issue. 4,
p.
333.
Havas, George
and
Newman, M. F.
1980.
Burnside Groups.
Vol. 806,
Issue. ,
p.
211.
Havas, George
1981.
Commutators in groups expressed as products of powers.
Communications in Algebra,
Vol. 9,
Issue. 2,
p.
115.
Bludov, V. V.
and
Kokorin, A. I.
1983.
Use of computers in solving well-known algebra problems.
Cybernetics,
Vol. 18,
Issue. 6,
p.
819.
Havas, George
and
Richardson, J.S.
1983.
Groups of exponent five and class four.
Communications in Algebra,
Vol. 11,
Issue. 3,
p.
287.