Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T05:58:55.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Covering groups of non-connected topological groups revisited

Published online by Cambridge University Press:  24 October 2008

Ronald Brown  and
Osman Mucuk
Ronald Brown
Affiliation:
School of Mathematics, University of Wales, Bangor, Gwynedd LL57 IUT
Osman Mucuk
Affiliation:
School of Mathematics, University of Wales, Bangor, Gwynedd LL57 IUT
Get access Rights & Permissions [Opens in a new window]

Extract

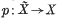All spaces are assumed to be locally path connected and semi-locally 1-connected. Let X be a connected topological group with identity e, and let be the universal cover of the underlying space of X. It follows easily from classical properties of lifting maps to covering spaces that for any point ẽ in 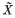with pẽ = e there is a unique structure of topological group on 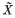such that ẽ is the identity and 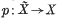is a morphism of groups. We say that the structure of topological group on X lifts to .

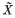Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 115 , Issue 1 , January 1994 , pp. 97 - 110
Copyright
Copyright © Cambridge Philosophical Society 1994

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1]Berrick, A. J.. Group extensions and their trivialisation. L'Enséignement Mathémalique 31 (1985), 151–172.Google Scholar
[2]Brown, R.. Fibrations of groupoids. J. Algebra 15 (1970), 103–132.CrossRefGoogle Scholar
[3]Brown, R.. Topology: a geometric account of general topology, homotopy types and the fundamental groupoid (Ellis Horwood, Chichester; Prentice Hall, New York, 1988).Google Scholar
[4]Brown, R. and Higgins, P. J.. Crossed complexes and non-abelian extensions. In Category Theory Proceedings, Gummersbach, 1981, Lecture Notes in Math. 962, edited Kamps, K. H.el al. (Springer, 1982).Google Scholar
[5]Brown, R. and Higgins, P. J.. Homotopies and tensor products for ω-groupoids and crossed complexes. J. Pure Appl. Algebra 47 (1987), 1–33.CrossRefGoogle Scholar
[6]Brown, R. and Higgins, P. J.. The classifying space of a crossed complex. Math. Proc. Cambridge Phil. Soc. 110 (1991), 95–120.CrossRefGoogle Scholar
[7]Brown, R. and Huebschmann, J.. Identities among relations, in Low-Dimensional Topology, eds. Brown, R. and Thickstun, T. L., London Math. Soc. Lecture Notes 48 (Cambridge University Press, 1982).CrossRefGoogle Scholar
[8]Brown, R. and Mackenzie, K.. Determination of a double Lie groupoid by its core diagram. J. Pure App. Algebra 80 (1992), 237–272.CrossRefGoogle Scholar
[9]Brown, R. and Spencer, C. B., G-groupoids, crossed modules and the fundamental groupoid of a topological group. Proc. Konn. Ned. Akad. v. Wet. 79 (1976), 296–302.Google Scholar
[10]Dedecker, P.. Les foncteurs non abéliens. C.R. Acad. Sci. Paris 258 (1964), 4891–4894.Google Scholar
[11]Higgins, P. J.. Categories and groupoids (Van Nostrand, 1971).Google Scholar
[12]Howie, J.. Pullback functors and fibrations of crossed complexes. Cah. Top. Ge'om. Diff. Cat. 20 (1979), 284–296.Google Scholar
[13]Huebschmann, J.. Crossed n-fold extensions and cohomology. Comm. Math. Helv. 55 (1980), 302–314.CrossRefGoogle Scholar
[14]Huebschmann, J.. Holonomies of Yang–Mills connections over a surface (PUB IRMA Lille, 26 No 9, 21 pp, 1991).Google Scholar
[15]Mackenzie, K.. Classification of principal bundles and Lie groupoids with prescribed gauge group bundle. J. Pure Appl. Algebra 58 (1989), 181–208.CrossRefGoogle Scholar
[16]MacLane, S.. Homology (Springer-Verlag, 1963).CrossRefGoogle Scholar
[17]Mucuk, O.. Covering groups of non-connected topological groups, and the monodromy groupoid of a topological groupoid. University of Wales PhD Thesis (Bangor, 1993).Google Scholar
[18]Taylor, R. L.. Compound group extensions I. Trans. Amer. Math. Soc. 75 (1953), 106–135.CrossRefGoogle Scholar
[19]Taylor, R. L.. Covering groups of non-connected topological groups. Proc. Amer. Math. Soc. 5 (1954), 753–768.CrossRefGoogle Scholar
[20]Whitehead, J. H. C.. Combinatorial homotopy II. Bull. Amer. Math. Soc. 55 (1949), 453–496.CrossRefGoogle Scholar