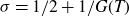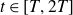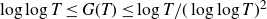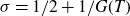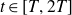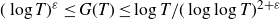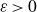1. Introduction
We investigate the distribution of the Riemann zeta function
![]() $ \zeta(s)$
for
$ \zeta(s)$
for
![]() $ \text{Re}(s) > 1/2$
using its probabilistic model defined by the random Euler product
$ \text{Re}(s) > 1/2$
using its probabilistic model defined by the random Euler product
 \begin{align*} \zeta( \sigma, \mathbb{X}) = \prod_p \bigg( 1 - \frac{ \mathbb{X}(p)}{ p^\sigma } \bigg)^{-1}, \end{align*}
\begin{align*} \zeta( \sigma, \mathbb{X}) = \prod_p \bigg( 1 - \frac{ \mathbb{X}(p)}{ p^\sigma } \bigg)^{-1}, \end{align*}
where the
![]() $ \mathbb{X}(p)$
for primes p are the uniform, independent and identically distributed random variables on the unit circle in
$ \mathbb{X}(p)$
for primes p are the uniform, independent and identically distributed random variables on the unit circle in
![]() $\mathbb{C}$
. The product converges almost surely for
$\mathbb{C}$
. The product converges almost surely for
![]() $ \sigma > 1/2 $
by Kolmogorov’s three series theorem. Our main question is how well the distribution of
$ \sigma > 1/2 $
by Kolmogorov’s three series theorem. Our main question is how well the distribution of
![]() $\zeta(\sigma, \mathbb{X})$
approximate that of the Riemann zeta function for
$\zeta(\sigma, \mathbb{X})$
approximate that of the Riemann zeta function for
![]() $ 1/2 < \sigma < 1 $
.
$ 1/2 < \sigma < 1 $
.
Consider two measures
and
for a Borel set
![]() $ \mathcal B$
in
$ \mathcal B$
in
![]() $\mathbb C$
. Define the discrepancy between the above two measures by
$\mathbb C$
. Define the discrepancy between the above two measures by
where
![]() $\mathcal R$
runs over all rectangular boxes in
$\mathcal R$
runs over all rectangular boxes in
![]() $\mathbb{C}$
with sides parallel to the coordinate axes and possibly unbounded. This quantity measures the amount to which the distribution of
$\mathbb{C}$
with sides parallel to the coordinate axes and possibly unbounded. This quantity measures the amount to which the distribution of
![]() $ \log \zeta( \sigma, \mathbb{X})$
approximates that of
$ \log \zeta( \sigma, \mathbb{X})$
approximates that of
![]() $ \log \zeta ( \sigma + it ) $
.
$ \log \zeta ( \sigma + it ) $
.
Harman and Matsumoto [ Reference Harman and Matsumoto2 ] showed that
for fixed
![]() $ 1/2 < \sigma < 1 $
and any
$ 1/2 < \sigma < 1 $
and any
![]() $\varepsilon > 0 $
. See also Matsumoto’s earlier results in [
Reference Matsumoto10–Reference Matsumoto12
]. Lamzouri, Lester and Radziwiłł [
Reference Lamzouri, Lester and Radziwiłł5
] improved it to
$\varepsilon > 0 $
. See also Matsumoto’s earlier results in [
Reference Matsumoto10–Reference Matsumoto12
]. Lamzouri, Lester and Radziwiłł [
Reference Lamzouri, Lester and Radziwiłł5
] improved it to
for fixed
![]() $ 1/2 < \sigma < 1 $
. Define
$ 1/2 < \sigma < 1 $
. Define
with
![]() $ 4 \leq G(T) \leq ( \log T)^\theta$
and fixed
$ 4 \leq G(T) \leq ( \log T)^\theta$
and fixed
![]() $ 0 < \theta < 1/2 $
, then Ha and Lee [
Reference Ha and Lee1
] extended above results such that
$ 0 < \theta < 1/2 $
, then Ha and Lee [
Reference Ha and Lee1
] extended above results such that
holds for some
![]() $ 0 < \eta < ({1- \theta})/{4} $
. Here, we extend it to hold for
$ 0 < \eta < ({1- \theta})/{4} $
. Here, we extend it to hold for
![]() $ \sigma_T $
closer to
$ \sigma_T $
closer to
![]() $ 1/2 $
.
$ 1/2 $
.
Theorem 1·1. Assume that
![]() $ \log \log T \leq G(T) \leq { \log T}/{ ( \log \log T)^2 } $
, then we have
$ \log \log T \leq G(T) \leq { \log T}/{ ( \log \log T)^2 } $
, then we have
Next we consider a multivariate extension. Let
![]() $L_1, \ldots, L_J$
be L-functions satisfying the following assumptions:
$L_1, \ldots, L_J$
be L-functions satisfying the following assumptions:
-
A1: (Euler product) For
 $ j = 1, \ldots, J $
and
$ j = 1, \ldots, J $
and
 $\text{Re}(s)>1$
we have where
$\text{Re}(s)>1$
we have where \begin{align*} L_j ( s) = \prod_p \prod_{i=1}^d \bigg( 1 - \frac{ \alpha_{j,i}(p)}{p^s} \bigg)^{-1}, \end{align*}
\begin{align*} L_j ( s) = \prod_p \prod_{i=1}^d \bigg( 1 - \frac{ \alpha_{j,i}(p)}{p^s} \bigg)^{-1}, \end{align*}
 $ | \alpha_{j,i} (p) | \leq p^{\eta}$
for some fixed
$ | \alpha_{j,i} (p) | \leq p^{\eta}$
for some fixed
 $ 0 \leq \eta < 1/2 $
and for every
$ 0 \leq \eta < 1/2 $
and for every
 $ i = 1, \ldots, d.$
$ i = 1, \ldots, d.$
-
A2: (Analytic continuation) Each
 $(s-1)^m L_j (s) $
is an entire function of finite order for some integer
$(s-1)^m L_j (s) $
is an entire function of finite order for some integer
 $ m \geq 0$
.
$ m \geq 0$
. -
A3: (Functional equation) The functions
 $L_1, L_2, \ldots, L_J$
satisfy the same functional equation where
$L_1, L_2, \ldots, L_J$
satisfy the same functional equation where \begin{align*} \Lambda_j(s) = \omega \overline{ \Lambda_j( 1- \bar{s})}, \end{align*}
\begin{align*} \Lambda_j(s) = \omega \overline{ \Lambda_j( 1- \bar{s})}, \end{align*}
 \begin{align*} \Lambda_j(s) \;:\!=\; L_j(s) Q^s \prod_{\ell=1}^k \Gamma ( \lambda_{\ell} s+\mu_{\ell} ), \end{align*}
\begin{align*} \Lambda_j(s) \;:\!=\; L_j(s) Q^s \prod_{\ell=1}^k \Gamma ( \lambda_{\ell} s+\mu_{\ell} ), \end{align*}
 $ | \omega| =1 $
,
$ | \omega| =1 $
,
 $Q>0$
,
$Q>0$
,
 $ \lambda_{\ell}>0 $
and
$ \lambda_{\ell}>0 $
and
 $\mu_{\ell} \in \mathbb{C} $
with
$\mu_{\ell} \in \mathbb{C} $
with
 $ \text{Re} ( \mu_{\ell} ) \geq 0 $
.
$ \text{Re} ( \mu_{\ell} ) \geq 0 $
.
-
A4: (Ramanujan hypothesis on average)
holds for every \begin{align*} \sum_{ p \leq x } \sum_{i=1}^d | \alpha_{j,i }(p) |^2 = O( x^{1+\varepsilon})\end{align*}
\begin{align*} \sum_{ p \leq x } \sum_{i=1}^d | \alpha_{j,i }(p) |^2 = O( x^{1+\varepsilon})\end{align*}
 $ \varepsilon>0$
and for every
$ \varepsilon>0$
and for every
 $ j = 1, \ldots, J $
as
$ j = 1, \ldots, J $
as
 $ x \to \infty $
.
$ x \to \infty $
.
-
A5: (Zero density hypothesis) Let
 $N_{f } ( \sigma, T )$
be the number of zeros of f (s) in
$N_{f } ( \sigma, T )$
be the number of zeros of f (s) in
 $\text{Re}(s) \geq \sigma$
and
$\text{Re}(s) \geq \sigma$
and
 $ 0 \leq \text{Im}(s) \leq T$
. Then there exists a constant
$ 0 \leq \text{Im}(s) \leq T$
. Then there exists a constant
 $\kappa >0$
such that for every
$\kappa >0$
such that for every
 $j= 1, \ldots, J$
and all
$j= 1, \ldots, J$
and all
 $\sigma\geq 1/2 $
we have
$\sigma\geq 1/2 $
we have  \begin{align*} N_{L_j } ( \sigma, T ) \ll T^{1 - \kappa (\sigma - \frac12 ) } \log T .\end{align*}
\begin{align*} N_{L_j } ( \sigma, T ) \ll T^{1 - \kappa (\sigma - \frac12 ) } \log T .\end{align*}
-
A6: (Selberg orthogonality conjecture) By assumption A1 we can write
Then for all \begin{align*} \log L_j(s) = \sum_p \sum_{r=1}^\infty \frac{ \beta_{L_j} (p^r)}{ p^{rs}} . \end{align*}
\begin{align*} \log L_j(s) = \sum_p \sum_{r=1}^\infty \frac{ \beta_{L_j} (p^r)}{ p^{rs}} . \end{align*}
 $1\leq j, k \leq J$
, there exist constants
$1\leq j, k \leq J$
, there exist constants
 $ \xi_j >0$
and
$ \xi_j >0$
and
 $ c_{j,k}$
such that where
$ c_{j,k}$
such that where \begin{align*} \sum_{p \leq x} \frac{ \beta_{L_j}(p) \overline{\beta_{L_k}(p) } }{p} = \delta_{j,k} \xi_j \log \log x + c_{j,k} + O \bigg( \frac{1}{ \log x} \bigg),\end{align*}
\begin{align*} \sum_{p \leq x} \frac{ \beta_{L_j}(p) \overline{\beta_{L_k}(p) } }{p} = \delta_{j,k} \xi_j \log \log x + c_{j,k} + O \bigg( \frac{1}{ \log x} \bigg),\end{align*}
 $ \delta_{j,k} = 0 $
if
$ \delta_{j,k} = 0 $
if
 $ j \neq k $
and
$ j \neq k $
and
 $ \delta_{j,k} = 1 $
if
$ \delta_{j,k} = 1 $
if
 $ j = k$
.
$ j = k$
.
The assumptions A1–A6 are standard and expected to hold for all L-functions arising from inequivalent automorphic representations of GL(n). In particular, they are verified by GL(1) and GL(2) L-functions, which are the Riemann zeta function, Dirichlet L-functions, L-functions attached to Hecke holomorphic or Maass cusp forms.
Define
and
for
![]() $ \sigma > 1/2$
, where
$ \sigma > 1/2$
, where
 \begin{equation} L_j ( \sigma, \mathbb{X}) \;:\!=\; \prod_p \prod_{i=1}^d \bigg( 1 - \frac{ \alpha_{j,i}(p) \mathbb{X}(p) }{p^\sigma} \bigg)^{-1} \end{equation}
\begin{equation} L_j ( \sigma, \mathbb{X}) \;:\!=\; \prod_p \prod_{i=1}^d \bigg( 1 - \frac{ \alpha_{j,i}(p) \mathbb{X}(p) }{p^\sigma} \bigg)^{-1} \end{equation}
converges almost surely for
![]() $ \sigma > 1/2$
again by Kolmogorov’s three series theorem. Then
$ \sigma > 1/2$
again by Kolmogorov’s three series theorem. Then
![]() $ \mathbf{L} ( \sigma, \mathbb{X}) $
is the random model of
$ \mathbf{L} ( \sigma, \mathbb{X}) $
is the random model of
![]() $ \mathbf{L} ( s)$
. Define two measures
$ \mathbf{L} ( s)$
. Define two measures
and
for a Borel set
![]() $ \mathcal B$
in
$ \mathcal B$
in
![]() $\mathbb R^{2J}$
and
$\mathbb R^{2J}$
and
![]() $ \sigma_T$
defined in (1·1). The discrepancy between the above two measures is defined by
$ \sigma_T$
defined in (1·1). The discrepancy between the above two measures is defined by
where
![]() $\mathcal R$
runs over all rectangular boxes of
$\mathcal R$
runs over all rectangular boxes of
![]() $ \mathbb{R}^{2J}$
with sides parallel to the coordinate axes and possibly unbounded. Then Theorem 1·1 is a special case of the following theorem.
$ \mathbb{R}^{2J}$
with sides parallel to the coordinate axes and possibly unbounded. Then Theorem 1·1 is a special case of the following theorem.
Theorem 1·2. Assume that
![]() $ \log \log T \leq G(T) \leq { \log T}/{ ( \log \log T)^2 } $
, then we have
$ \log \log T \leq G(T) \leq { \log T}/{ ( \log \log T)^2 } $
, then we have
The above theorem is an extension of [
Reference Lamzouri and Lee4
, theorem 2·3], which shows the same estimate, but only for
![]() $ \log \log T \leq G(T) \leq { \sqrt{ \log T}}/{ \log \log T} $
. In the proof of [
Reference Lamzouri and Lee4
, theorem 2·3] we have used an approximation of each
$ \log \log T \leq G(T) \leq { \sqrt{ \log T}}/{ \log \log T} $
. In the proof of [
Reference Lamzouri and Lee4
, theorem 2·3] we have used an approximation of each
![]() $\log L_j ( \sigma_T + it )$
by a Dirichlet polynomial
$\log L_j ( \sigma_T + it )$
by a Dirichlet polynomial
 \begin{equation} R_{j, Y} ( \sigma_T + i t ) \;:\!=\; \sum_{ p^r \leq Y} \frac{ \beta_{L_j} ( p^r) }{p^{r ( \sigma_T + it)}} \end{equation}
\begin{equation} R_{j, Y} ( \sigma_T + i t ) \;:\!=\; \sum_{ p^r \leq Y} \frac{ \beta_{L_j} ( p^r) }{p^{r ( \sigma_T + it)}} \end{equation}
for
![]() $t \in [T, 2T]$
with some exception. The exception essentially comes from possible nontrivial zeros of each
$t \in [T, 2T]$
with some exception. The exception essentially comes from possible nontrivial zeros of each
![]() $L_j (s)$
off the critical line and the set of exceptional t in [T,2T] has a small measure by assumption A5. See [
Reference Lamzouri and Lee4
, lemma 4·2] for details. However, this approximation is not useful if
$L_j (s)$
off the critical line and the set of exceptional t in [T,2T] has a small measure by assumption A5. See [
Reference Lamzouri and Lee4
, lemma 4·2] for details. However, this approximation is not useful if
![]() $ \sigma_T$
is closer to
$ \sigma_T$
is closer to
![]() $ 1/2 $
. We overcome such difficulty by means of the 2nd moment estimation of
$ 1/2 $
. We overcome such difficulty by means of the 2nd moment estimation of
![]() $ \log L_j (\sigma_T + it )$
in Theorem 2·1.
$ \log L_j (\sigma_T + it )$
in Theorem 2·1.
As an application of Theorem 1·2 we consider Selberg’s central limit theorem. Let
![]() $ \psi_{j,T} \;:\!=\; \xi_j \log G( T) $
for
$ \psi_{j,T} \;:\!=\; \xi_j \log G( T) $
for
![]() $ j \leq J$
and
$ j \leq J$
and
 \begin{align*} {\mathcal{R}_T} \;:\!=\; \prod_{j=1}^J [ a_j \sqrt{ \pi \psi_{j, T}}, b_j \sqrt{ \pi \psi_{j, T}}] \times \prod_{j=1}^J [ c_j \sqrt{ \pi \psi_{j, T}}, d_j \sqrt{ \pi \psi_{j, T}}] \end{align*}
\begin{align*} {\mathcal{R}_T} \;:\!=\; \prod_{j=1}^J [ a_j \sqrt{ \pi \psi_{j, T}}, b_j \sqrt{ \pi \psi_{j, T}}] \times \prod_{j=1}^J [ c_j \sqrt{ \pi \psi_{j, T}}, d_j \sqrt{ \pi \psi_{j, T}}] \end{align*}
for fixed real numbers
![]() $ a_j, b_j, c_j, d_j$
. Then an asymptotic formula for
$ a_j, b_j, c_j, d_j$
. Then an asymptotic formula for
is called Selberg’s central limit theorem. See [
Reference Selberg15
, theorem 2] for Selberg’s original idea. Let
![]() $0 < \theta < 1 $
. To find an asymptotic of
$0 < \theta < 1 $
. To find an asymptotic of
![]() $ \Phi_T ( {\mathcal{R}_T} )$
for
$ \Phi_T ( {\mathcal{R}_T} )$
for
it is now enough to estimate
![]() $ \Phi_T^{\textrm{rand}} ( {\mathcal{R}_T})$
due to Theorem 1·2. One can easily check that the asymptotic formula of
$ \Phi_T^{\textrm{rand}} ( {\mathcal{R}_T})$
due to Theorem 1·2. One can easily check that the asymptotic formula of
![]() $ \Phi_T^{\textrm{rand}} ( {\mathcal{R}_T})$
in [
Reference Lee9
, theorem 2·1] holds also for G(T) satisfying (1·6). Hence, we obtain the following corollary.
$ \Phi_T^{\textrm{rand}} ( {\mathcal{R}_T})$
in [
Reference Lee9
, theorem 2·1] holds also for G(T) satisfying (1·6). Hence, we obtain the following corollary.
Corollary 1·3. Assume (1·6) for some
![]() $ 0< \theta < 1$
and assumptions A1–A6 for
$ 0< \theta < 1$
and assumptions A1–A6 for
![]() $L_1, \ldots, L_J $
. Then there exist constants
$L_1, \ldots, L_J $
. Then there exist constants
![]() $\varepsilon_1, \varepsilon_2 > 0$
and a sequence
$\varepsilon_1, \varepsilon_2 > 0$
and a sequence
![]() $ \{ b_{\mathbf{k}, \mathbf{l}}\}$
of real numbers such that
$ \{ b_{\mathbf{k}, \mathbf{l}}\}$
of real numbers such that
 \begin{equation}\begin{split} \Phi_T ( {\mathcal{R}_T} ) = & \sum_{ \mathcal{K}( \mathbf{k}+\mathbf{l}) \leq \varepsilon_1 \log\log T } b_{\mathbf{k}, \mathbf{l}} \prod_{j=1}^J \frac{1}{ \sqrt{\psi_{j,T} }^{k_j + \ell_j } } \\ & \times \prod_{j=1}^J \bigg( \int_{a_j}^{b_j} e^{ - \pi u^2 } \mathcal{H}_{k_j } ( \sqrt{\pi}u )du \int_{c_j}^{d_j} e^{ - \pi v^2 } \mathcal{H}_{\ell_j } ( \sqrt{\pi}v )dv \bigg) \\& + O \bigg( \frac{1}{ ( \log T)^{\varepsilon_2}} + \frac{\sqrt{G(T)} \log \log T }{ \sqrt{ \log T}} \bigg), \end{split}\end{equation}
\begin{equation}\begin{split} \Phi_T ( {\mathcal{R}_T} ) = & \sum_{ \mathcal{K}( \mathbf{k}+\mathbf{l}) \leq \varepsilon_1 \log\log T } b_{\mathbf{k}, \mathbf{l}} \prod_{j=1}^J \frac{1}{ \sqrt{\psi_{j,T} }^{k_j + \ell_j } } \\ & \times \prod_{j=1}^J \bigg( \int_{a_j}^{b_j} e^{ - \pi u^2 } \mathcal{H}_{k_j } ( \sqrt{\pi}u )du \int_{c_j}^{d_j} e^{ - \pi v^2 } \mathcal{H}_{\ell_j } ( \sqrt{\pi}v )dv \bigg) \\& + O \bigg( \frac{1}{ ( \log T)^{\varepsilon_2}} + \frac{\sqrt{G(T)} \log \log T }{ \sqrt{ \log T}} \bigg), \end{split}\end{equation}
where
![]() $ \mathbf{k} = ( k_1, \ldots, k_J) $
and
$ \mathbf{k} = ( k_1, \ldots, k_J) $
and
![]() $ \mathbf{l} = ( \ell_1, \ldots, \ell_J)$
are vectors in
$ \mathbf{l} = ( \ell_1, \ldots, \ell_J)$
are vectors in
![]() $(\mathbb{Z}_{\geq 0})^J $
,
$(\mathbb{Z}_{\geq 0})^J $
,
![]() $ \mathcal{K}(\mathbf{k} ) \;:\!=\; k_1 + \cdots +k_J $
and
$ \mathcal{K}(\mathbf{k} ) \;:\!=\; k_1 + \cdots +k_J $
and
is the nth Hermite polynomial. Moreover,
![]() $b_{0,0}= 1 $
,
$b_{0,0}= 1 $
,
![]() $ b_{\mathbf{k}, \mathbf{l}} = 0 $
if
$ b_{\mathbf{k}, \mathbf{l}} = 0 $
if
![]() $ \mathcal{K}(\mathbf{k} + \mathbf{l}) = 1$
and
$ \mathcal{K}(\mathbf{k} + \mathbf{l}) = 1$
and
![]() $b_{\mathbf{k}, \mathbf{l} } = O( \delta_0^{- \mathcal{K}(\mathbf{k}+\mathbf{l})})$
for some
$b_{\mathbf{k}, \mathbf{l} } = O( \delta_0^{- \mathcal{K}(\mathbf{k}+\mathbf{l})})$
for some
![]() $ \delta_0 > 0$
and all
$ \delta_0 > 0$
and all
![]() $ \mathbf{k}, \mathbf{l} \in (\mathbb{Z}_{\geq 0})^J $
.
$ \mathbf{k}, \mathbf{l} \in (\mathbb{Z}_{\geq 0})^J $
.
Note that Corollary 1·3 extends the asymptotic expansion for
![]() $ \zeta (s) $
in [
Reference Lee8
, theorem 1·2] and the asymptotic expansion for
$ \zeta (s) $
in [
Reference Lee8
, theorem 1·2] and the asymptotic expansion for
![]() $\mathbf{L} (s)$
in [
Reference Lee9
, theorem 1·2]. If G(T) is very close to
$\mathbf{L} (s)$
in [
Reference Lee9
, theorem 1·2]. If G(T) is very close to
![]() $ { \log T}/{ ( \log \log T )^2 }$
, the error term in (1·7) is large so that we have an approximation by a shorter sum as follows.
$ { \log T}/{ ( \log \log T )^2 }$
, the error term in (1·7) is large so that we have an approximation by a shorter sum as follows.
Corollary 1·4. Under the same assumptions as in Corollary 1·3 except for
with a constant
![]() $ g > 0 $
, we have
$ g > 0 $
, we have
 \begin{align*} \Phi_T ( {\mathcal{R}_T} ) = & \sum_{ \mathcal{K}( \mathbf{k}+\mathbf{l}) < g } b_{\mathbf{k}, \mathbf{l}} \prod_{j=1}^J \frac{1}{ \sqrt{\psi_{j,T} }^{k_j + \ell_j } } \\ & \times \prod_{j=1}^J \bigg( \int_{a_j}^{b_j} e^{ - \pi u^2 } \mathcal{H}_{k_j } ( \sqrt{\pi}u )du \int_{c_j}^{d_j} e^{ - \pi v^2 } \mathcal{H}_{\ell_j } ( \sqrt{\pi}v )dv \bigg) + O \bigg( \frac{1}{ ( \log \log T )^{ \frac{g}{2} }} \bigg) . \end{align*}
\begin{align*} \Phi_T ( {\mathcal{R}_T} ) = & \sum_{ \mathcal{K}( \mathbf{k}+\mathbf{l}) < g } b_{\mathbf{k}, \mathbf{l}} \prod_{j=1}^J \frac{1}{ \sqrt{\psi_{j,T} }^{k_j + \ell_j } } \\ & \times \prod_{j=1}^J \bigg( \int_{a_j}^{b_j} e^{ - \pi u^2 } \mathcal{H}_{k_j } ( \sqrt{\pi}u )du \int_{c_j}^{d_j} e^{ - \pi v^2 } \mathcal{H}_{\ell_j } ( \sqrt{\pi}v )dv \bigg) + O \bigg( \frac{1}{ ( \log \log T )^{ \frac{g}{2} }} \bigg) . \end{align*}
Note that an asymptotic expansion similar to (1·7) was expected to hold in [ Reference Hejhal3 ] without a proof.
2. High moments of
 $ \log L$
$ \log L$
Let L be an L-function satisfying assumptions A1–A6 in this section. Here, we use
![]() $ \alpha_i (p)$
instead of
$ \alpha_i (p)$
instead of
![]() $\alpha_{j,i}(p)$
in assumptions A1 and A4, and assumption A6 is simply
$\alpha_{j,i}(p)$
in assumptions A1 and A4, and assumption A6 is simply
 \begin{align*} \sum_{p \leq x} \frac{ | \beta_{L }(p) |^2 }{p} = \xi_L \log \log x + c_L + O \bigg( \frac{1}{ \log x} \bigg)\end{align*}
\begin{align*} \sum_{p \leq x} \frac{ | \beta_{L }(p) |^2 }{p} = \xi_L \log \log x + c_L + O \bigg( \frac{1}{ \log x} \bigg)\end{align*}
for some constants
![]() $ \xi_L >0 $
and
$ \xi_L >0 $
and
![]() $ c_L \in \mathbb{R}$
. Let
$ c_L \in \mathbb{R}$
. Let
![]() $\sigma_T $
be defined in (1·1) and assume that
$\sigma_T $
be defined in (1·1) and assume that
in this section. Then we need the following theorem to prove Theorem 1·2.
Theorem 2·1. Let
![]() $\kappa $
be as in assumption A5 and
$\kappa $
be as in assumption A5 and
![]() $ 0< \varepsilon < \min\{ 1/{48}, {\kappa}/3 \} $
. Assume (2·1) and
$ 0< \varepsilon < \min\{ 1/{48}, {\kappa}/3 \} $
. Assume (2·1) and
![]() $ e^{ \frac{G(T)}{2}} \leq Y \leq T^{ \varepsilon } $
, then there exists
$ e^{ \frac{G(T)}{2}} \leq Y \leq T^{ \varepsilon } $
, then there exists
![]() $ \kappa_0 > 0 $
such that
$ \kappa_0 > 0 $
such that
where
To prove above theorem, we modify high moments estimations of
![]() $\log \zeta$
in Tsang’s thesis [
Reference Tsang16
] and compute high moments of
$\log \zeta$
in Tsang’s thesis [
Reference Tsang16
] and compute high moments of
![]() $\log L$
. All these computations are based on Selberg [
Reference Selberg13, Reference Selberg14
]. Since the Dirichlet coefficients of L(s) are allowed to be larger than 1, Theorem 2·1 is not an immediate consequence of Tsang [
Reference Tsang16
]. We need to bound various sums involving the Dirichlet coefficients of
$\log L$
. All these computations are based on Selberg [
Reference Selberg13, Reference Selberg14
]. Since the Dirichlet coefficients of L(s) are allowed to be larger than 1, Theorem 2·1 is not an immediate consequence of Tsang [
Reference Tsang16
]. We need to bound various sums involving the Dirichlet coefficients of
![]() $\log L$
carefully using assumptions A4 and A6. As a result we obtain the following theorem.
$\log L$
carefully using assumptions A4 and A6. As a result we obtain the following theorem.
Theorem 2·2. Let
![]() $\kappa $
be as in assumption A5 and
$\kappa $
be as in assumption A5 and
![]() $ 0< \varepsilon < \min\{ 1/{48}, {\kappa}/3 \} $
. Let k be a positive integer such that
$ 0< \varepsilon < \min\{ 1/{48}, {\kappa}/3 \} $
. Let k be a positive integer such that
![]() $ k \leq ({\varepsilon}/{4}) ( \log \log T )^2 $
Assume (2·1), then there exist
$ k \leq ({\varepsilon}/{4}) ( \log \log T )^2 $
Assume (2·1), then there exist
![]() $\kappa_0, c >0$
such that
$\kappa_0, c >0$
such that
and
By Theorem 2·2 with
![]() $ k= \log \log T$
one can easily derive the following corollary, which is necessary in Section 3.
$ k= \log \log T$
one can easily derive the following corollary, which is necessary in Section 3.
Corollary 2·3 Assume (2·1). Given constant
![]() $ A_1 >0$
, there exists a constant
$ A_1 >0$
, there exists a constant
![]() $A_2 >0$
such that
$A_2 >0$
such that
and
We provide lemmas in Section 2·1 and then prove Theorems 2·1 and 2·2 in Section 2·2
2·1. Lemmas
We adapt estimations in [
Reference Tsang16
, chapter 5] for
![]() $ \log L$
. We begin with [
Reference Tsang16
, lemma 5·1].
$ \log L$
. We begin with [
Reference Tsang16
, lemma 5·1].
Lemma 2·4. Let
![]() $\kappa$
be as in assumption A5,
$\kappa$
be as in assumption A5,
![]() $ 0 < \kappa' < \kappa $
and
$ 0 < \kappa' < \kappa $
and
![]() $ \nu \geq 0 $
. Then there is a constant
$ \nu \geq 0 $
. Then there is a constant
![]() $ c> 0 $
such that
$ c> 0 $
such that
 \begin{align*} \sum_{ \substack{ \beta > \sigma \\ T \leq \gamma \leq 2 T}} ( \beta - \sigma)^\nu X^{ \beta- \sigma} = O \big( T^{1 - \kappa (\sigma - \frac12 ) } ( \log T)^{1 - \nu} (c\nu)^\nu \big) \end{align*}
\begin{align*} \sum_{ \substack{ \beta > \sigma \\ T \leq \gamma \leq 2 T}} ( \beta - \sigma)^\nu X^{ \beta- \sigma} = O \big( T^{1 - \kappa (\sigma - \frac12 ) } ( \log T)^{1 - \nu} (c\nu)^\nu \big) \end{align*}
for
![]() $ 1/2 \leq \sigma \leq 1 $
and
$ 1/2 \leq \sigma \leq 1 $
and
![]() $ 3 \leq X \leq T^{\kappa - \kappa'} $
, where
$ 3 \leq X \leq T^{\kappa - \kappa'} $
, where
![]() $ \beta+i\gamma$
denotes a zero of L(s).
$ \beta+i\gamma$
denotes a zero of L(s).
Proof. We only prove the case
![]() $ \nu > 0 $
, since the case
$ \nu > 0 $
, since the case
![]() $ \nu = 0 $
is similar. First we see that
$ \nu = 0 $
is similar. First we see that
 \begin{align*}\sum_{ \substack{ \beta > \sigma \\ T \leq \gamma \leq 2 T}} ( \beta - \sigma)^\nu X^{ \beta- \sigma} & = \sum_{ \substack{ \beta > \sigma \\ T \leq \gamma \leq 2 T}} \int_0^{ \beta - \sigma} d( u^\nu X^u ) = \int_0^{ 1 - \sigma} \sum_{ \substack{ \beta > \sigma +u \\ T \leq \gamma \leq 2 T}} d( u^\nu X^u ) \\& \leq \int_0^{ 1 - \sigma} N_L( \sigma +u , 2T) d( u^\nu X^u ) .\end{align*}
\begin{align*}\sum_{ \substack{ \beta > \sigma \\ T \leq \gamma \leq 2 T}} ( \beta - \sigma)^\nu X^{ \beta- \sigma} & = \sum_{ \substack{ \beta > \sigma \\ T \leq \gamma \leq 2 T}} \int_0^{ \beta - \sigma} d( u^\nu X^u ) = \int_0^{ 1 - \sigma} \sum_{ \substack{ \beta > \sigma +u \\ T \leq \gamma \leq 2 T}} d( u^\nu X^u ) \\& \leq \int_0^{ 1 - \sigma} N_L( \sigma +u , 2T) d( u^\nu X^u ) .\end{align*}
By assumption A5, the above is
 \begin{align*}\ll & T^{1 - \kappa(\sigma - \frac12 ) } \log T \int_0^{ 1 - \sigma} T^{-\kappa u } ( \nu u^{\nu -1 } X^u + u^{\nu } X^u \log X ) du \\\leq & T^{1 - \kappa(\sigma - \frac12 ) } \log T \int_0^{ \infty } ( \nu u^{\nu -1 } + u^{\nu } \log X ) T^{-\kappa' u } du \\\ll & T^{1 - \kappa(\sigma - \frac12 ) } ( \log T )^{1- \nu} c^\nu \Gamma(\nu+1 )\end{align*}
\begin{align*}\ll & T^{1 - \kappa(\sigma - \frac12 ) } \log T \int_0^{ 1 - \sigma} T^{-\kappa u } ( \nu u^{\nu -1 } X^u + u^{\nu } X^u \log X ) du \\\leq & T^{1 - \kappa(\sigma - \frac12 ) } \log T \int_0^{ \infty } ( \nu u^{\nu -1 } + u^{\nu } \log X ) T^{-\kappa' u } du \\\ll & T^{1 - \kappa(\sigma - \frac12 ) } ( \log T )^{1- \nu} c^\nu \Gamma(\nu+1 )\end{align*}
for some
![]() $ c > 0 $
. Hence, the lemma follows.
$ c > 0 $
. Hence, the lemma follows.
Define
for
![]() $ t \in [T, 2T]$
, where the maximum is taken over all zeros
$ t \in [T, 2T]$
, where the maximum is taken over all zeros
![]() $ \beta + i \gamma$
of L(s) satisfying
$ \beta + i \gamma$
of L(s) satisfying
![]() $ | t- \gamma | \leq { x^{ 3 ( \beta - 1/2)}}/{ \log x } $
and
$ | t- \gamma | \leq { x^{ 3 ( \beta - 1/2)}}/{ \log x } $
and
![]() $ \beta \geq 1/2$
. Then the following lemma corresponds to [
Reference Tsang16
, lemma 5·2].
$ \beta \geq 1/2$
. Then the following lemma corresponds to [
Reference Tsang16
, lemma 5·2].
Lemma 2·5. Let
![]() $ \nu \geq 0$
,
$ \nu \geq 0$
,
![]() $ 0 < \kappa' < \kappa$
and
$ 0 < \kappa' < \kappa$
and
![]() $ x = T^{ \varepsilon/k} $
for
$ x = T^{ \varepsilon/k} $
for
![]() $ \varepsilon, k >0$
. Suppose that
$ \varepsilon, k >0$
. Suppose that
![]() $3 \leq x^3 X^2 \leq T^{\kappa - \kappa' }$
. Then there is a constant
$3 \leq x^3 X^2 \leq T^{\kappa - \kappa' }$
. Then there is a constant
![]() $ c>0$
depending on
$ c>0$
depending on
![]() $\kappa, \varepsilon$
such that
$\kappa, \varepsilon$
such that
for
![]() $ 1/2 + {4}/{ \log x} \leq \sigma \leq 1 $
and
$ 1/2 + {4}/{ \log x} \leq \sigma \leq 1 $
and
 \begin{align*}\int_{\substack{ \sigma_{x,t} > \sigma \\ T \leq t \leq 2T}} ( \sigma_{x,t} - \sigma)^\nu X^{ \sigma_{x,t} - \sigma} dt \ll_{\varepsilon} & \frac{ (c\nu)^\nu k }{ ( \log T)^{ \nu} } T^{1 - \frac{ \kappa}{2} (\sigma - \frac12 ) } + T \frac{c^{k+\nu} k^\nu }{ (\log T)^\nu }\end{align*}
\begin{align*}\int_{\substack{ \sigma_{x,t} > \sigma \\ T \leq t \leq 2T}} ( \sigma_{x,t} - \sigma)^\nu X^{ \sigma_{x,t} - \sigma} dt \ll_{\varepsilon} & \frac{ (c\nu)^\nu k }{ ( \log T)^{ \nu} } T^{1 - \frac{ \kappa}{2} (\sigma - \frac12 ) } + T \frac{c^{k+\nu} k^\nu }{ (\log T)^\nu }\end{align*}
for
![]() $ 1/2 \leq \sigma \leq 1/2 + {4}/{ \log x} $
.
$ 1/2 \leq \sigma \leq 1/2 + {4}/{ \log x} $
.
Proof. Define two sets
 \begin{align*} S_1 &= \left\{ t \in [T, 2T ] : \sigma_{x,t} > \max \left( \sigma, \frac12 + \frac{4}{ \log x} \right) \right\}, \\ S_2 &= \left\{ t \in [T, 2T ] : \sigma_{x,t} = \frac12 + \frac{4}{ \log x} > \sigma \right\} . \end{align*}
\begin{align*} S_1 &= \left\{ t \in [T, 2T ] : \sigma_{x,t} > \max \left( \sigma, \frac12 + \frac{4}{ \log x} \right) \right\}, \\ S_2 &= \left\{ t \in [T, 2T ] : \sigma_{x,t} = \frac12 + \frac{4}{ \log x} > \sigma \right\} . \end{align*}
Since
![]() $\sigma_{x,t} \geq 1/2 + \frac{4}{ \log x}$
, we see that
$\sigma_{x,t} \geq 1/2 + \frac{4}{ \log x}$
, we see that
For
![]() $ t \in S_1 $
, by the definition of
$ t \in S_1 $
, by the definition of
![]() $\sigma_{x,t}$
and
$\sigma_{x,t}$
and
![]() $ \sigma_{x, t}> 1/2 + {4}/{ \log x} $
, there exists a zero
$ \sigma_{x, t}> 1/2 + {4}/{ \log x} $
, there exists a zero
![]() $ \beta+ i \gamma$
such that
$ \beta+ i \gamma$
such that
![]() $\sigma_{x,t} = 2 \beta - 1/2 $
,
$\sigma_{x,t} = 2 \beta - 1/2 $
,
![]() $ \beta - 1/2 > {2}/{ \log x}$
and
$ \beta - 1/2 > {2}/{ \log x}$
and
![]() $ | t- \gamma | \leq { x^{ 3 ( \beta - 1/2)}}/{ \log x } $
. Thus, we have
$ | t- \gamma | \leq { x^{ 3 ( \beta - 1/2)}}/{ \log x } $
. Thus, we have
 \begin{align*} \int_{S_1} ( \sigma_{x,t} - \sigma)^\nu X^{ \sigma_{x,t} - \sigma} dt & \leq \sum_{ \substack{ \beta > \frac12( \sigma + \frac12 ) \\ \frac{T}{2} \leq \gamma \leq 3T }} \int_{ \gamma - \frac{ x^{ 3 ( \beta - \frac12)}}{ \log x } }^{ \gamma + \frac{ x^{ 3 ( \beta - \frac12)}}{ \log x } } \bigg( 2 \beta - \frac12 - \sigma \bigg)^\nu X^{ 2 \beta - \frac12 - \sigma} dt \\& \leq \frac{ 2^{1+\nu} x^{ \frac32 ( \sigma - \frac12)}}{ \log x } \sum_{ \substack{ \beta > \frac12( \sigma + \frac12 ) \\ \frac{T}{2} \leq \gamma \leq 3T }} \bigg( \beta - \frac12 \bigg( \sigma + \frac12 \bigg)\bigg)^\nu (x^3 X^2)^{ \beta - \frac12( \sigma + \frac12 ) } .\end{align*}
\begin{align*} \int_{S_1} ( \sigma_{x,t} - \sigma)^\nu X^{ \sigma_{x,t} - \sigma} dt & \leq \sum_{ \substack{ \beta > \frac12( \sigma + \frac12 ) \\ \frac{T}{2} \leq \gamma \leq 3T }} \int_{ \gamma - \frac{ x^{ 3 ( \beta - \frac12)}}{ \log x } }^{ \gamma + \frac{ x^{ 3 ( \beta - \frac12)}}{ \log x } } \bigg( 2 \beta - \frac12 - \sigma \bigg)^\nu X^{ 2 \beta - \frac12 - \sigma} dt \\& \leq \frac{ 2^{1+\nu} x^{ \frac32 ( \sigma - \frac12)}}{ \log x } \sum_{ \substack{ \beta > \frac12( \sigma + \frac12 ) \\ \frac{T}{2} \leq \gamma \leq 3T }} \bigg( \beta - \frac12 \bigg( \sigma + \frac12 \bigg)\bigg)^\nu (x^3 X^2)^{ \beta - \frac12( \sigma + \frac12 ) } .\end{align*}
By Lemma 2·4 the above is
for some
![]() $c>0$
.
$c>0$
.
We see that
![]() $S_2 = \emptyset$
for
$S_2 = \emptyset$
for
![]() $ \sigma \geq 1/2 + {4}/{ \log x }$
. If
$ \sigma \geq 1/2 + {4}/{ \log x }$
. If
![]() $ 1/2 \leq \sigma \leq 1/2 + {4}/{ \log x }$
, then
$ 1/2 \leq \sigma \leq 1/2 + {4}/{ \log x }$
, then
for some
![]() $c>0$
.
$c>0$
.
Next we consider [
Reference Tsang16
, lemma 5·3] and observe that the condition (ii) therein does not hold in our setting. To adapt its proof to our setting, it requires several inequalities regarding
![]() $ \beta_L$
. By assumptions A1 and A6 we have
$ \beta_L$
. By assumptions A1 and A6 we have
 \begin{equation} \beta_{L} (p^r ) = \frac1r \sum_{i=1}^d \alpha_{i}(p)^r . \end{equation}
\begin{equation} \beta_{L} (p^r ) = \frac1r \sum_{i=1}^d \alpha_{i}(p)^r . \end{equation}
From (2·5) and assumption A1 it is easy to derive that
 \begin{equation} | \beta_{L } (p^r) | \leq \frac1r \sum_{i=1}^d | \alpha_{i}(p)|^r \leq \frac{p^{(r-2)\eta}}{r} \sum_{i=1}^d |\alpha_{i} (p)|^2 \quad \textrm{for\;} r \geq 2 \end{equation}
\begin{equation} | \beta_{L } (p^r) | \leq \frac1r \sum_{i=1}^d | \alpha_{i}(p)|^r \leq \frac{p^{(r-2)\eta}}{r} \sum_{i=1}^d |\alpha_{i} (p)|^2 \quad \textrm{for\;} r \geq 2 \end{equation}
and
 \begin{equation}| \beta_{L} (p ) |^2 \leq \bigg( \sum_{i=1}^d | \alpha_{i}(p)| \bigg)^2 \leq d \sum_{i=1}^d |\alpha_{i} (p)|^2 . \end{equation}
\begin{equation}| \beta_{L} (p ) |^2 \leq \bigg( \sum_{i=1}^d | \alpha_{i}(p)| \bigg)^2 \leq d \sum_{i=1}^d |\alpha_{i} (p)|^2 . \end{equation}
For convenience we extend
![]() $ \beta_L$
by letting
$ \beta_L$
by letting
![]() $ \beta_L (n) = 0 $
if n is not a power of a prime. Then we see that
$ \beta_L (n) = 0 $
if n is not a power of a prime. Then we see that
Define
for
![]() $ \sigma \in [ 1/2, 1]$
and
$ \sigma \in [ 1/2, 1]$
and
 \begin{align*} g_x (n) \;:\!=\;\begin{cases}1 & \textrm{for} \; 1 \leq n \leq x, \\ \frac{ \log^2 ( x^3/n) - 2 \log^2 ( x^2 / n ) }{2 \log^2 x } & \textrm{for} \; x \leq n \leq x^2, \\ \frac{ \log^2 ( x^3 / n ) }{ 2\log^2 x } & \textrm{for} \; x^2 \leq n \leq x^3, \\ 0 & \textrm{for} \; x^3 \leq n, \end{cases} \end{align*}
\begin{align*} g_x (n) \;:\!=\;\begin{cases}1 & \textrm{for} \; 1 \leq n \leq x, \\ \frac{ \log^2 ( x^3/n) - 2 \log^2 ( x^2 / n ) }{2 \log^2 x } & \textrm{for} \; x \leq n \leq x^2, \\ \frac{ \log^2 ( x^3 / n ) }{ 2\log^2 x } & \textrm{for} \; x^2 \leq n \leq x^3, \\ 0 & \textrm{for} \; x^3 \leq n, \end{cases} \end{align*}
then we have the following lemma.
Lemma 2·6. Let k and m be positive integers such that
![]() $ k \leq m \leq 16 k $
,
$ k \leq m \leq 16 k $
,
![]() $\kappa$
as in assumption A5 and
$\kappa$
as in assumption A5 and
![]() $ x = T^{ \frac{\varepsilon}{k}} $
. Assume that
$ x = T^{ \frac{\varepsilon}{k}} $
. Assume that
![]() $ { \varepsilon}/{k} < {\kappa}/{3} $
and
$ { \varepsilon}/{k} < {\kappa}/{3} $
and
![]() $0 < \varepsilon \leq 1/{48}$
. Then there exists a constant
$0 < \varepsilon \leq 1/{48}$
. Then there exists a constant
![]() $c>0$
such that
$c>0$
such that
 \begin{align*} \int_T^{2T} \bigg| \sum_{ n } \frac{ \beta_L (n) g_x(n) }{ n^{ \lambda_t +it}} \bigg|^{2m} dt \ll T c^k k^m \bigg( \min\bigg\{ \log \log x, \log \frac{1}{ \sigma - \frac12 } \bigg\} \bigg)^m \end{align*}
\begin{align*} \int_T^{2T} \bigg| \sum_{ n } \frac{ \beta_L (n) g_x(n) }{ n^{ \lambda_t +it}} \bigg|^{2m} dt \ll T c^k k^m \bigg( \min\bigg\{ \log \log x, \log \frac{1}{ \sigma - \frac12 } \bigg\} \bigg)^m \end{align*}
and
 \begin{align*} \int_T^{2T} \bigg| \sum_{ n } \frac{ \beta_L (n) g_x(n) \log n }{ n^{ \lambda_t +it}} \bigg|^{2m} dt \ll T c^k k^m \bigg( \min \bigg\{ \log x, \frac{1}{ \sigma - \frac12} \bigg\} \bigg)^{2 m } \end{align*}
\begin{align*} \int_T^{2T} \bigg| \sum_{ n } \frac{ \beta_L (n) g_x(n) \log n }{ n^{ \lambda_t +it}} \bigg|^{2m} dt \ll T c^k k^m \bigg( \min \bigg\{ \log x, \frac{1}{ \sigma - \frac12} \bigg\} \bigg)^{2 m } \end{align*}
for
![]() $ 1/2 \leq \sigma \leq 1 $
.
$ 1/2 \leq \sigma \leq 1 $
.
Proof. Let
![]() $ \ell$
be a nonnegative integer, then we see that
$ \ell$
be a nonnegative integer, then we see that
We split the first sum on the right-hand side as
 \begin{align*} \sum_{ n } \frac{ \beta_L (n) g_x(n)( \log n)^\ell }{ n^{ \sigma +it}} = & \sum_{ p } \frac{ \beta_L (p) g_x(p) ( \log p)^\ell}{ p^{ \sigma +it}}+\sum_{ p } \frac{ \beta_L (p^2 ) g_x(p^2 ) ( 2 \log p)^\ell}{ p^{ 2\sigma +2it}} \\ &+\sum_{p}\sum_{ r \geq 3 } \frac{ \beta_L (p^r ) g_x(p^r ) ( r\log p)^\ell}{ p^{ r\sigma +irt}} . \end{align*}
\begin{align*} \sum_{ n } \frac{ \beta_L (n) g_x(n)( \log n)^\ell }{ n^{ \sigma +it}} = & \sum_{ p } \frac{ \beta_L (p) g_x(p) ( \log p)^\ell}{ p^{ \sigma +it}}+\sum_{ p } \frac{ \beta_L (p^2 ) g_x(p^2 ) ( 2 \log p)^\ell}{ p^{ 2\sigma +2it}} \\ &+\sum_{p}\sum_{ r \geq 3 } \frac{ \beta_L (p^r ) g_x(p^r ) ( r\log p)^\ell}{ p^{ r\sigma +irt}} . \end{align*}
By (2·7) and assumption A4 we have
 \begin{align*} \bigg| \sum_{p}\sum_{ r \geq 3 } \frac{ \beta_L (p^r ) g_x(p^r ) (r \log p)^\ell }{ p^{ r\sigma +irt}} \bigg| & \leq \sum_{p}\sum_{ 3 \leq r \leq \frac{ 3 \log x}{ \log p} } \frac{ p^{(r-2)\eta }\sum_{i=1}^d |\alpha_i (p )|^2 ( r \log p)^\ell }{ r p^{ r\sigma }} \\ & \ll \sum_{p} \frac{ \sum_{i=1}^d |\alpha_i (p )|^2 ( \log p)^\ell }{ p^{ \frac32 - \eta }} \ll 1 .\end{align*}
\begin{align*} \bigg| \sum_{p}\sum_{ r \geq 3 } \frac{ \beta_L (p^r ) g_x(p^r ) (r \log p)^\ell }{ p^{ r\sigma +irt}} \bigg| & \leq \sum_{p}\sum_{ 3 \leq r \leq \frac{ 3 \log x}{ \log p} } \frac{ p^{(r-2)\eta }\sum_{i=1}^d |\alpha_i (p )|^2 ( r \log p)^\ell }{ r p^{ r\sigma }} \\ & \ll \sum_{p} \frac{ \sum_{i=1}^d |\alpha_i (p )|^2 ( \log p)^\ell }{ p^{ \frac32 - \eta }} \ll 1 .\end{align*}
By [ Reference Tsang16 , lemma 3·3] we have
 \begin{align*} \int_T^{2T} \bigg| \sum_{ p } \frac{ \beta_L (p) g_x(p) ( \log p)^\ell}{ p^{ \sigma +it}} \bigg|^{2m} dt & \ll T m! \bigg( \sum_{ p } \frac{ |\beta_L (p) g_x(p)|^2 ( \log p)^{2\ell} }{ p^{ 2 \sigma }} \bigg)^m \\ \int_T^{2T} \bigg| \sum_{ p } \frac{ \beta_L (p^2) g_x(p^2)( \log p)^\ell }{ p^{ 2\sigma +2 it}} \bigg|^{2m} dt & \ll T m! \bigg( \sum_{ p } \frac{ |\beta_L (p^2) g_x(p^2)|^2 ( \log p)^{2\ell}}{ p^{ 4 \sigma }} \bigg)^m \end{align*}
\begin{align*} \int_T^{2T} \bigg| \sum_{ p } \frac{ \beta_L (p) g_x(p) ( \log p)^\ell}{ p^{ \sigma +it}} \bigg|^{2m} dt & \ll T m! \bigg( \sum_{ p } \frac{ |\beta_L (p) g_x(p)|^2 ( \log p)^{2\ell} }{ p^{ 2 \sigma }} \bigg)^m \\ \int_T^{2T} \bigg| \sum_{ p } \frac{ \beta_L (p^2) g_x(p^2)( \log p)^\ell }{ p^{ 2\sigma +2 it}} \bigg|^{2m} dt & \ll T m! \bigg( \sum_{ p } \frac{ |\beta_L (p^2) g_x(p^2)|^2 ( \log p)^{2\ell}}{ p^{ 4 \sigma }} \bigg)^m \end{align*}
provided that
![]() $x^{3m } \ll T$
, which holds for
$x^{3m } \ll T$
, which holds for
![]() $ 0< \varepsilon \leq 1/{48}$
. By assumption A6 we have
$ 0< \varepsilon \leq 1/{48}$
. By assumption A6 we have
 \begin{align*} \sum_{ p } \frac{ |\beta_L (p) g_x(p)|^2 ( \log p)^{2\ell} }{ p^{ 2 \sigma }} \leq \sum_{ p \leq x^3 } \frac{ |\beta_L (p) |^2 ( \log p)^{2\ell} }{ p } \ll \begin{cases} \log \log x & \textrm{if}\; \ell=0, \\ (\log x)^{2\ell } & \textrm{if}\; \ell \geq 1 \end{cases} \end{align*}
\begin{align*} \sum_{ p } \frac{ |\beta_L (p) g_x(p)|^2 ( \log p)^{2\ell} }{ p^{ 2 \sigma }} \leq \sum_{ p \leq x^3 } \frac{ |\beta_L (p) |^2 ( \log p)^{2\ell} }{ p } \ll \begin{cases} \log \log x & \textrm{if}\; \ell=0, \\ (\log x)^{2\ell } & \textrm{if}\; \ell \geq 1 \end{cases} \end{align*}
for
![]() $ 1/2 \leq \sigma \leq 1/2 + {4}/{ \log x} $
,
$ 1/2 \leq \sigma \leq 1/2 + {4}/{ \log x} $
,
 \begin{align*} \sum_{ p } \frac{ |\beta_L (p) g_x(p)|^2 ( \log p)^{2\ell} }{ p^{ 2 \sigma }}& \leq \sum_{ p } \frac{ |\beta_L (p) |^2 ( \log p)^{2\ell} }{ p^{2 \sigma} } \ll \int_2^\infty u^{-2\sigma}(\log u )^{2\ell-1} du \\ & \ll \begin{cases} \log \frac{1}{ \sigma - \frac12 } & \textrm{if}\; \ell=0,\\ \frac{1}{ ( \sigma - \frac12 )^{2 \ell }} & \textrm{if}\; \ell \geq 1 \end{cases} \end{align*}
\begin{align*} \sum_{ p } \frac{ |\beta_L (p) g_x(p)|^2 ( \log p)^{2\ell} }{ p^{ 2 \sigma }}& \leq \sum_{ p } \frac{ |\beta_L (p) |^2 ( \log p)^{2\ell} }{ p^{2 \sigma} } \ll \int_2^\infty u^{-2\sigma}(\log u )^{2\ell-1} du \\ & \ll \begin{cases} \log \frac{1}{ \sigma - \frac12 } & \textrm{if}\; \ell=0,\\ \frac{1}{ ( \sigma - \frac12 )^{2 \ell }} & \textrm{if}\; \ell \geq 1 \end{cases} \end{align*}
for
![]() $ 1/2 + {4}/{ \log x} \leq \sigma \leq 1 $
. By (2·7) and assumption A4 we have
$ 1/2 + {4}/{ \log x} \leq \sigma \leq 1 $
. By (2·7) and assumption A4 we have
 \begin{align*}\sum_{ p } \frac{ |\beta_L (p^2) g_x(p^2)|^2 (\log p)^{2\ell}}{ p^{ 4 \sigma }} \ll \sum_{ p } \frac{ \sum_{i=1}^d |\alpha_i (p ) |^2 (\log p)^{2\ell}}{ p^{ 2-2 \eta }} \ll 1\end{align*}
\begin{align*}\sum_{ p } \frac{ |\beta_L (p^2) g_x(p^2)|^2 (\log p)^{2\ell}}{ p^{ 4 \sigma }} \ll \sum_{ p } \frac{ \sum_{i=1}^d |\alpha_i (p ) |^2 (\log p)^{2\ell}}{ p^{ 2-2 \eta }} \ll 1\end{align*}
for
![]() $ \sigma \geq 1/2 $
. Since
$ \sigma \geq 1/2 $
. Since
 \begin{multline*} \bigg| \sum_{ n } \frac{ \beta_L (n) g_x(n) (\log n)^\ell }{ n^{ \sigma +it}} \bigg|^{2m} \\ \leq 3^m \bigg( \bigg|\sum_{ p } \frac{ \beta_L (p) g_x(p) (\log p)^{\ell} }{ p^{ \sigma +it}} \bigg|^{2m} + \bigg| \sum_{ p } \frac{ \beta_L (p^2 ) g_x(p^2 ) (2 \log p )^{\ell}}{ p^{ 2\sigma +2it}}\bigg|^{2m} + c^m \bigg)\end{multline*}
\begin{multline*} \bigg| \sum_{ n } \frac{ \beta_L (n) g_x(n) (\log n)^\ell }{ n^{ \sigma +it}} \bigg|^{2m} \\ \leq 3^m \bigg( \bigg|\sum_{ p } \frac{ \beta_L (p) g_x(p) (\log p)^{\ell} }{ p^{ \sigma +it}} \bigg|^{2m} + \bigg| \sum_{ p } \frac{ \beta_L (p^2 ) g_x(p^2 ) (2 \log p )^{\ell}}{ p^{ 2\sigma +2it}}\bigg|^{2m} + c^m \bigg)\end{multline*}
for some
![]() $c>0$
, by collecting above equations we find that
$c>0$
, by collecting above equations we find that
 \begin{equation} \begin{split}\int_T^{2T}& \bigg| \sum_{ n } \frac{ \beta_L (n) g_x(n) (\log n)^\ell }{ n^{ \sigma +it}} \bigg|^{2m} dt\\ & \ll \begin{cases} T c^k k^m \bigg( \min\bigg\{ \log \log x, \log \frac{1}{ \sigma - \frac12 } \bigg\} \bigg)^m & \textrm{if}\; \ell=0, \\ T c^k k^m \bigg( \min \bigg\{ \log x, \frac{1}{ \sigma - \frac12} \bigg\} \bigg)^{2 \ell m } & \textrm{if}\; \ell \geq 1 \end{cases}\end{split}\end{equation}
\begin{equation} \begin{split}\int_T^{2T}& \bigg| \sum_{ n } \frac{ \beta_L (n) g_x(n) (\log n)^\ell }{ n^{ \sigma +it}} \bigg|^{2m} dt\\ & \ll \begin{cases} T c^k k^m \bigg( \min\bigg\{ \log \log x, \log \frac{1}{ \sigma - \frac12 } \bigg\} \bigg)^m & \textrm{if}\; \ell=0, \\ T c^k k^m \bigg( \min \bigg\{ \log x, \frac{1}{ \sigma - \frac12} \bigg\} \bigg)^{2 \ell m } & \textrm{if}\; \ell \geq 1 \end{cases}\end{split}\end{equation}
for some constant
![]() $c>0$
and for
$c>0$
and for
![]() $ 1/2 \leq \sigma \leq 1 $
.
$ 1/2 \leq \sigma \leq 1 $
.
We next estimate
By equations in [ Reference Tsang16 , p. 67] the above integral is bounded by
 \begin{align*}\ll &\bigg( \int_T^{2T} ( \lambda_t - \sigma)^{4m} X_1^{4m(\lambda_t - \sigma)} dt \bigg)^{\frac12} \bigg( \int_{\sigma}^\infty X_1^{\sigma-v} dv \bigg)^{2m-\frac12}\\& \times \bigg( \int_\sigma^\infty X_1^{\sigma-v} \int_T^{2T} \bigg| \sum_{n} \frac{ \beta_L(n) g_x(n) (\log n )^{\ell+1} \log ( X_1 n )}{ n^{ v+it}} \bigg|^{4m} dt dv \bigg)^{\frac12}\end{align*}
\begin{align*}\ll &\bigg( \int_T^{2T} ( \lambda_t - \sigma)^{4m} X_1^{4m(\lambda_t - \sigma)} dt \bigg)^{\frac12} \bigg( \int_{\sigma}^\infty X_1^{\sigma-v} dv \bigg)^{2m-\frac12}\\& \times \bigg( \int_\sigma^\infty X_1^{\sigma-v} \int_T^{2T} \bigg| \sum_{n} \frac{ \beta_L(n) g_x(n) (\log n )^{\ell+1} \log ( X_1 n )}{ n^{ v+it}} \bigg|^{4m} dt dv \bigg)^{\frac12}\end{align*}
with
![]() $ X_1= T^{\frac{\varepsilon_1 }{m}} $
for some
$ X_1= T^{\frac{\varepsilon_1 }{m}} $
for some
![]() $ \varepsilon_1 >0$
. Let
$ \varepsilon_1 >0$
. Let
![]() $ \nu= 4m $
and
$ \nu= 4m $
and
![]() $ X = X_1^{4m} = T^{4 \varepsilon_1 } $
in Lemma 2·5. One can easily check that the assumptions in Lemma 2·5 follow from the assumptions in Lemma 2·6. Thus, by Lemma 2·5 there exists
$ X = X_1^{4m} = T^{4 \varepsilon_1 } $
in Lemma 2·5. One can easily check that the assumptions in Lemma 2·5 follow from the assumptions in Lemma 2·6. Thus, by Lemma 2·5 there exists
![]() $c>0$
such that
$c>0$
such that
for
![]() $ 1/2 \leq \sigma \leq 1 $
. By (2·9) we have
$ 1/2 \leq \sigma \leq 1 $
. By (2·9) we have
 \begin{align*}\int_\sigma^\infty & X_1^{\sigma-v} \int_T^{2T} \bigg| \sum_{n} \frac{ \beta_L(n) g_x(n)(\log n)^{\ell+1} \log ( X_1 n )}{ n^{ v+it}} \bigg|^{4m} dt dv \\& \ll T c^k k^{2m} \bigg( \frac{ \log T}{k}\bigg)^{2m(2\ell+3) -1 } \bigg(\min \bigg\{ \log x, \frac{1}{ \sigma - \frac12} \bigg\} \bigg)^{2m} .\end{align*}
\begin{align*}\int_\sigma^\infty & X_1^{\sigma-v} \int_T^{2T} \bigg| \sum_{n} \frac{ \beta_L(n) g_x(n)(\log n)^{\ell+1} \log ( X_1 n )}{ n^{ v+it}} \bigg|^{4m} dt dv \\& \ll T c^k k^{2m} \bigg( \frac{ \log T}{k}\bigg)^{2m(2\ell+3) -1 } \bigg(\min \bigg\{ \log x, \frac{1}{ \sigma - \frac12} \bigg\} \bigg)^{2m} .\end{align*}
Therefore, by combining above results we obtain
 \begin{multline} \int_T^{2T} \bigg| \sum_{ n } \frac{ \beta_L (n) g_x(n) (\log n)^\ell }{ n^{ it}} ( n^{- \lambda_t} - n^{- \sigma}) \bigg|^{2m} dt \\ \ll c^k k^{ 2m -2m\ell } T^{ 1 - \frac{ 1}{4} (\kappa - \frac{3 \varepsilon}{k} )( \sigma - \frac12 )} ( \log T)^{ 2m\ell - m } \bigg(\min \bigg\{ \log x, \frac{1}{ \sigma - \frac12} \bigg\} \bigg)^{m} \end{multline}
\begin{multline} \int_T^{2T} \bigg| \sum_{ n } \frac{ \beta_L (n) g_x(n) (\log n)^\ell }{ n^{ it}} ( n^{- \lambda_t} - n^{- \sigma}) \bigg|^{2m} dt \\ \ll c^k k^{ 2m -2m\ell } T^{ 1 - \frac{ 1}{4} (\kappa - \frac{3 \varepsilon}{k} )( \sigma - \frac12 )} ( \log T)^{ 2m\ell - m } \bigg(\min \bigg\{ \log x, \frac{1}{ \sigma - \frac12} \bigg\} \bigg)^{m} \end{multline}
for
![]() $ 1/2 \leq \sigma \leq 1 $
. The lemma follows from (2·9) and (2·10).
$ 1/2 \leq \sigma \leq 1 $
. The lemma follows from (2·9) and (2·10).
The following lemma is an analogy of [ Reference Tsang16 , lemma 5·4]. The proof of [ Reference Lee7 , lemma 8] is for Hecke L-functions of number fields, but it works also for our L-functions. So we state the lemma without a proof.
Lemma 2·7 Let
![]() $ t \in [T, 2T] $
,
$ t \in [T, 2T] $
,
![]() $ 1/2 \leq \sigma \leq 1 $
and
$ 1/2 \leq \sigma \leq 1 $
and
![]() $t \neq \text{Im}(\rho)$
for any zeros
$t \neq \text{Im}(\rho)$
for any zeros
![]() $\rho$
of L(s). Then we have:
$\rho$
of L(s). Then we have:
 \begin{multline*} \log L(s) = \sum_n \frac{ \beta_L (n) g_x(n)}{ n^{ \lambda_t + it}} + \tilde{L} (s) \\ + O \bigg( \bigg( \frac{ x^{ \frac14 - \frac12 \lambda_t}}{ \log x} + ( \lambda_t - \sigma) \bigg)\bigg( \bigg| \sum_n \frac{ \beta_L (n) g_x(n) \log n }{ n^{ \sigma_{x,t} + it}} \bigg| + \log T \bigg)\bigg),\end{multline*}
\begin{multline*} \log L(s) = \sum_n \frac{ \beta_L (n) g_x(n)}{ n^{ \lambda_t + it}} + \tilde{L} (s) \\ + O \bigg( \bigg( \frac{ x^{ \frac14 - \frac12 \lambda_t}}{ \log x} + ( \lambda_t - \sigma) \bigg)\bigg( \bigg| \sum_n \frac{ \beta_L (n) g_x(n) \log n }{ n^{ \sigma_{x,t} + it}} \bigg| + \log T \bigg)\bigg),\end{multline*}
where
 \begin{equation} \tilde{L} ( s) = \sum_{\rho} \int_\sigma^{\lambda_t} \frac{ u- \lambda_t}{ (u+it-\rho)(\lambda_t + it - \rho)} du . \end{equation}
\begin{equation} \tilde{L} ( s) = \sum_{\rho} \int_\sigma^{\lambda_t} \frac{ u- \lambda_t}{ (u+it-\rho)(\lambda_t + it - \rho)} du . \end{equation}
The following lemma is proved for the Riemann zeta function in the proof of [ Reference Tsang16 , lemma 5·5]. We rewrite its proof for convenience.
Lemma 2·8 Let
![]() $\tilde{L}(s)$
be as in (2·11) and
$\tilde{L}(s)$
be as in (2·11) and
![]() $ x = T^{\frac{ \varepsilon}{k}}$
. Assume that
$ x = T^{\frac{ \varepsilon}{k}}$
. Assume that
![]() $ { \varepsilon}/{k} < {\kappa}/{3} $
and
$ { \varepsilon}/{k} < {\kappa}/{3} $
and
![]() $0 < \varepsilon \leq 1/{48}$
. Then we have
$0 < \varepsilon \leq 1/{48}$
. Then we have
 \begin{align*}|\text{Im}( \tilde{L} (s)) | & \ll ( \lambda_t - \sigma) \bigg( \bigg| \sum_n \frac{ \beta_L (n) g_x(n) \log n }{ n^{ \lambda_t + it}}\bigg| + \log T \bigg), \\|\text{Re}(\tilde{L}(s))| & \ll ( \lambda_t - \sigma)\big( 1+ ( \lambda_t - \sigma) \log x + \log^+ \frac{1}{ \eta_t \log x } \big)\\ & \times \bigg( \bigg| \sum_n \frac{ \beta_L (n) g_x(n) \log n }{ n^{ \lambda_t + it}}\bigg| + \log T \bigg),\end{align*}
\begin{align*}|\text{Im}( \tilde{L} (s)) | & \ll ( \lambda_t - \sigma) \bigg( \bigg| \sum_n \frac{ \beta_L (n) g_x(n) \log n }{ n^{ \lambda_t + it}}\bigg| + \log T \bigg), \\|\text{Re}(\tilde{L}(s))| & \ll ( \lambda_t - \sigma)\big( 1+ ( \lambda_t - \sigma) \log x + \log^+ \frac{1}{ \eta_t \log x } \big)\\ & \times \bigg( \bigg| \sum_n \frac{ \beta_L (n) g_x(n) \log n }{ n^{ \lambda_t + it}}\bigg| + \log T \bigg),\end{align*}
where
![]() $ \log^+ w \;:\!=\; \max\{ \log w, 0 \} $
and
$ \log^+ w \;:\!=\; \max\{ \log w, 0 \} $
and
![]() $ \eta_t = \min | t-\gamma|$
with the minimum taken over all zeros
$ \eta_t = \min | t-\gamma|$
with the minimum taken over all zeros
![]() $ \beta+i \gamma $
of L(s) with
$ \beta+i \gamma $
of L(s) with
![]() $ \beta \geq 1/2$
. Moreover, we have
$ \beta \geq 1/2$
. Moreover, we have
for some
![]() $ c>0$
.
$ c>0$
.
Proof. If
![]() $ \sigma \geq \sigma_{x,t}$
, then
$ \sigma \geq \sigma_{x,t}$
, then
![]() $ \lambda_t = \sigma $
,
$ \lambda_t = \sigma $
,
![]() $ \tilde{L}(s) = 0 $
and the lemma holds trivially. Thus, we assume that
$ \tilde{L}(s) = 0 $
and the lemma holds trivially. Thus, we assume that
![]() $ \sigma < \sigma_{x,t}$
, then
$ \sigma < \sigma_{x,t}$
, then
![]() $ \lambda_t = \sigma_{x,t}$
. By (2·11) we find that
$ \lambda_t = \sigma_{x,t}$
. By (2·11) we find that
and
 \begin{equation} \text{Re} ( \tilde{L}(s)) =\sum_{\rho} \int_\sigma^{\sigma_{x,t}} \frac{ ( u- \sigma_{x,t} ) \big( (u-\beta) (\sigma_{x,t} - \beta) - ( t-\gamma)^2 \big) }{ | u+it-\rho |^2 | \sigma_{x,t} + it - \rho |^2 } du . \end{equation}
\begin{equation} \text{Re} ( \tilde{L}(s)) =\sum_{\rho} \int_\sigma^{\sigma_{x,t}} \frac{ ( u- \sigma_{x,t} ) \big( (u-\beta) (\sigma_{x,t} - \beta) - ( t-\gamma)^2 \big) }{ | u+it-\rho |^2 | \sigma_{x,t} + it - \rho |^2 } du . \end{equation}
First we find an upper bound of
![]() $ \text{Im} ( \tilde{L}(s))$
. By (2·12) and
$ \text{Im} ( \tilde{L}(s))$
. By (2·12) and
![]() $ | \sigma_{x,t} - u | \leq | \sigma_{x,t} - \sigma|$
, we have
$ | \sigma_{x,t} - u | \leq | \sigma_{x,t} - \sigma|$
, we have
 \begin{align*}| \text{Im} ( \tilde{L}(s)) | \leq & \sum_{\rho} \int_\sigma^{\sigma_{x,t}} \frac{ | \sigma_{x,t} -u | | t-\gamma | ( | \sigma_{x,t} -u| + 2 | u-\beta| ) }{ | u+it-\rho |^2 | \sigma_{x,t}+ it - \rho |^2 } du \\\leq & \sum_{\rho} \frac{ | \sigma_{x,t} - \sigma |^2 }{ | \sigma_{x,t}+ it - \rho |^2 } \int_\sigma^{\sigma_{x,t}} \frac{ | t-\gamma | }{ (u-\beta)^2 + ( t-\gamma)^2 } du \\& + 2 \sum_{\rho} \frac{ | \sigma_{x,t} -\sigma | }{ | \sigma_{x,t}+ it - \rho |^2} \int_\sigma^{\sigma_{x,t}} \frac{ | t-\gamma | | u-\beta| }{ (u-\beta)^2 + ( t-\gamma)^2 } du.\end{align*}
\begin{align*}| \text{Im} ( \tilde{L}(s)) | \leq & \sum_{\rho} \int_\sigma^{\sigma_{x,t}} \frac{ | \sigma_{x,t} -u | | t-\gamma | ( | \sigma_{x,t} -u| + 2 | u-\beta| ) }{ | u+it-\rho |^2 | \sigma_{x,t}+ it - \rho |^2 } du \\\leq & \sum_{\rho} \frac{ | \sigma_{x,t} - \sigma |^2 }{ | \sigma_{x,t}+ it - \rho |^2 } \int_\sigma^{\sigma_{x,t}} \frac{ | t-\gamma | }{ (u-\beta)^2 + ( t-\gamma)^2 } du \\& + 2 \sum_{\rho} \frac{ | \sigma_{x,t} -\sigma | }{ | \sigma_{x,t}+ it - \rho |^2} \int_\sigma^{\sigma_{x,t}} \frac{ | t-\gamma | | u-\beta| }{ (u-\beta)^2 + ( t-\gamma)^2 } du.\end{align*}
The integrals on the right-hand side are
 \begin{align*}\int_\sigma^{\sigma_{x,t}} \frac{ | t-\gamma | }{ (u-\beta)^2 + ( t-\gamma)^2 } du & \leq \int_{-\infty}^\infty \frac{ | t-\gamma | }{ (u-\beta)^2 + ( t-\gamma)^2 } du = \int_{-\infty}^\infty \frac{du}{u^2 + 1 } = \pi,\\\int_\sigma^{\sigma_{x,t}} \frac{ | t-\gamma | | u-\beta| }{ (u-\beta)^2 + ( t-\gamma)^2 } du & \leq ( \sigma_{x,t}- \sigma),\end{align*}
\begin{align*}\int_\sigma^{\sigma_{x,t}} \frac{ | t-\gamma | }{ (u-\beta)^2 + ( t-\gamma)^2 } du & \leq \int_{-\infty}^\infty \frac{ | t-\gamma | }{ (u-\beta)^2 + ( t-\gamma)^2 } du = \int_{-\infty}^\infty \frac{du}{u^2 + 1 } = \pi,\\\int_\sigma^{\sigma_{x,t}} \frac{ | t-\gamma | | u-\beta| }{ (u-\beta)^2 + ( t-\gamma)^2 } du & \leq ( \sigma_{x,t}- \sigma),\end{align*}
so that
 \begin{equation} | \text{Im} ( \tilde{L}(s)) | \leq ( \pi + 2 ) \sum_{\rho} \frac{ | \sigma_{x,t} - \sigma |^2 }{ | \sigma_{x,t}+ it - \rho |^2 } . \end{equation}
\begin{equation} | \text{Im} ( \tilde{L}(s)) | \leq ( \pi + 2 ) \sum_{\rho} \frac{ | \sigma_{x,t} - \sigma |^2 }{ | \sigma_{x,t}+ it - \rho |^2 } . \end{equation}
Selberg in (4·8) of [ Reference Selberg13 ] proved that
for the Riemann zeta function, and it also holds for our L-functions. We may prove (2·15) by (4·4) and (4·6) of [ Reference Lee7 ] in the proof of [ Reference Lee7 , lemma 8]. By (2·14) and (2·15) the first inequality in Lemma 2·8 holds.
Next we find an upper bound of
![]() $ \text{Re} ( \tilde{L}(s))$
. By (2·13), we have
$ \text{Re} ( \tilde{L}(s))$
. By (2·13), we have
 \begin{align*}| \text{Re} ( \tilde{L}(s)) | \leq & \sum_{\rho} \int_\sigma^{\sigma_{x,t}} \frac{ | \sigma_{x,t} - u | \big( |u-\beta| (|\sigma_{x,t}-u| +|u - \beta|) + | t-\gamma|^2 \big) }{ | u+it-\rho |^2 | \sigma_{x,t} + it - \rho |^2 } du\\ \leq & \sum_{\rho} \frac{ | \sigma_{x,t} - \sigma |^2 }{ | \sigma_{x,t} + it - \rho |^2 } \int_\sigma^{\sigma_{x,t}} \frac{ |u-\beta| }{ (u-\beta)^2 + ( t-\gamma)^2 } du + \sum_{\rho} \frac{ | \sigma_{x,t} - \sigma | }{ | \sigma_{x,t} + it - \rho |^2 } .\end{align*}
\begin{align*}| \text{Re} ( \tilde{L}(s)) | \leq & \sum_{\rho} \int_\sigma^{\sigma_{x,t}} \frac{ | \sigma_{x,t} - u | \big( |u-\beta| (|\sigma_{x,t}-u| +|u - \beta|) + | t-\gamma|^2 \big) }{ | u+it-\rho |^2 | \sigma_{x,t} + it - \rho |^2 } du\\ \leq & \sum_{\rho} \frac{ | \sigma_{x,t} - \sigma |^2 }{ | \sigma_{x,t} + it - \rho |^2 } \int_\sigma^{\sigma_{x,t}} \frac{ |u-\beta| }{ (u-\beta)^2 + ( t-\gamma)^2 } du + \sum_{\rho} \frac{ | \sigma_{x,t} - \sigma | }{ | \sigma_{x,t} + it - \rho |^2 } .\end{align*}
The integral on the right-hand side is
Define
![]() $ \log^+ w = \max\{ \log w, 0 \} $
for
$ \log^+ w = \max\{ \log w, 0 \} $
for
![]() $ w >0 $
, then for any
$ w >0 $
, then for any
![]() $ v, w > 0 $
, it is easy to verify
$ v, w > 0 $
, it is easy to verify
![]() $ \log (1+w) \leq 1 + \log^+ w $
,
$ \log (1+w) \leq 1 + \log^+ w $
,
![]() $ \log^+ ({w}/{v}) \leq \log^+ w + \log^+ ({1}/{v}) $
and
$ \log^+ ({w}/{v}) \leq \log^+ w + \log^+ ({1}/{v}) $
and
![]() $ \log^+w \leq w $
. Then we have
$ \log^+w \leq w $
. Then we have
 \begin{align*} \log \bigg( 1 + \frac{ \sigma_{x,t} - \sigma}{ |t-\gamma| } \bigg) \leq & \log \bigg( 1 + \frac{ (\sigma_{x,t} - \sigma)\log x }{ \eta_t \log x } \bigg) \\ \leq & 1 + \log^+ \big( ( \sigma_{x,t} - \sigma) \log x \big) + \log^+ \frac{1}{ \eta_t \log x } \\ \leq & 1+ ( \sigma_{x,t} - \sigma) \log x + \log^+ \frac{1}{ \eta_t \log x } .\end{align*}
\begin{align*} \log \bigg( 1 + \frac{ \sigma_{x,t} - \sigma}{ |t-\gamma| } \bigg) \leq & \log \bigg( 1 + \frac{ (\sigma_{x,t} - \sigma)\log x }{ \eta_t \log x } \bigg) \\ \leq & 1 + \log^+ \big( ( \sigma_{x,t} - \sigma) \log x \big) + \log^+ \frac{1}{ \eta_t \log x } \\ \leq & 1+ ( \sigma_{x,t} - \sigma) \log x + \log^+ \frac{1}{ \eta_t \log x } .\end{align*}
Thus, we find that
Now, the second inequality of Lemma 2·8 follows from the above inequality and (2·15).
By the definition of
![]() $ \log^+$
and
$ \log^+$
and
![]() $ \eta_t$
we find that
$ \eta_t$
we find that
 \begin{align*} \int_T^{2T} \left( \log^+ \frac{1}{ \eta_t \log x } \right)^{2k} dt \leq \sum_{ \substack{ \beta\geq \frac12 \\ T - \frac{1}{\log x} \leq \gamma \leq 2 T+ \frac{1}{\log x} }} \int_{0}^{ \frac{1}{\log x} } \bigg( \log^+ \frac{1}{ w \log x } \bigg)^{2k} dw . \end{align*}
\begin{align*} \int_T^{2T} \left( \log^+ \frac{1}{ \eta_t \log x } \right)^{2k} dt \leq \sum_{ \substack{ \beta\geq \frac12 \\ T - \frac{1}{\log x} \leq \gamma \leq 2 T+ \frac{1}{\log x} }} \int_{0}^{ \frac{1}{\log x} } \bigg( \log^+ \frac{1}{ w \log x } \bigg)^{2k} dw . \end{align*}
The number of zeros in the above sum is
![]() $ O( T \log T)$
. By substituting
$ O( T \log T)$
. By substituting
![]() $ w \log x = e^{-v}$
, the last integral equals to
$ w \log x = e^{-v}$
, the last integral equals to
![]() $ { \Gamma(2k+1)}/{ \log x} = { (2k)!}/{ \log x} $
. Hence, the last inequality of Lemma 2·8 follows.
$ { \Gamma(2k+1)}/{ \log x} = { (2k)!}/{ \log x} $
. Hence, the last inequality of Lemma 2·8 follows.
2·2. Proof of Theorems 2·1 and 2·2
To prove Theorems 2·1 and 2·2, we need to find an upper bound of the 2kth moment
 \begin{align*} \int_T^{2T} \bigg| \log L ( \sigma_T + it ) - \sum_{ n} \frac{ \beta_L (n) g_x (n) }{ n^{ \sigma_T + it }} \bigg|^{2k} dt, \end{align*}
\begin{align*} \int_T^{2T} \bigg| \log L ( \sigma_T + it ) - \sum_{ n} \frac{ \beta_L (n) g_x (n) }{ n^{ \sigma_T + it }} \bigg|^{2k} dt, \end{align*}
where
![]() $ x= T^{ ({ \varepsilon}/{k})}$
,
$ x= T^{ ({ \varepsilon}/{k})}$
,
![]() $ k \leq {\varepsilon}/{4} ( \log \log T)^2 $
and
$ k \leq {\varepsilon}/{4} ( \log \log T)^2 $
and
![]() $ 0< \varepsilon < \min\{1/{48}, {\kappa}/3 \} $
. Let
$ 0< \varepsilon < \min\{1/{48}, {\kappa}/3 \} $
. Let
![]() $\sigma = 1/2$
and
$\sigma = 1/2$
and
![]() $ k=m$
in Lemma 2·6, then we get
$ k=m$
in Lemma 2·6, then we get
 \begin{equation}\int_T^{2T} \bigg| \sum_n \frac{ \beta_L (n) g_x(n) \log n }{ n^{ \sigma_{x,t} + it}} \bigg|^{2k} dt \ll c^k k^k T ( \log x)^{2 k}.\end{equation}
\begin{equation}\int_T^{2T} \bigg| \sum_n \frac{ \beta_L (n) g_x(n) \log n }{ n^{ \sigma_{x,t} + it}} \bigg|^{2k} dt \ll c^k k^k T ( \log x)^{2 k}.\end{equation}
By Lemmas 2·7 and 2·8 and (2·16), we have
 \begin{equation}\begin{split}\int_T^{2T}& \bigg| \log L ( \sigma_T + it ) - \sum_{ n} \frac{ \beta_L (n) g_x (n) }{ n^{ \sigma_T + it }} \bigg|^{2k} dt \\\ll &\; c^k \int_T^{2T} \bigg| \sum_n \frac{ \beta_L (n) g_x(n)}{ n^{ \lambda_t + it}} - \sum_n \frac{ \beta_L (n) g_x(n)}{ n^{ \sigma_T + it}} \bigg|^{2k} dt \\+&\; c^k \int_T^{2T} ( \lambda_t - \sigma_T )^{2k}\bigg( 1+ ( \lambda_t - \sigma_T ) \log x + \log^+ \frac{1}{ \eta_t \log x } \bigg)^{2k} \\ \times &\;\bigg| \sum_n \frac{ \beta_L (n) g_x(n) \log n }{ n^{ \lambda_t + it}}\bigg|^{2k} dt \\+&\; c^k ( \log T)^{2k} \int_T^{2T} ( \lambda_t - \sigma_T )^{2k}\bigg( 1+ ( \lambda_t - \sigma_T ) \log x + \log^+ \frac{1}{ \eta_t \log x } \bigg)^{2k} dt \\+&\; c^k k^{2k} T e^{- \varepsilon \frac{ \log T}{ G(T)} }\end{split}\end{equation}
\begin{equation}\begin{split}\int_T^{2T}& \bigg| \log L ( \sigma_T + it ) - \sum_{ n} \frac{ \beta_L (n) g_x (n) }{ n^{ \sigma_T + it }} \bigg|^{2k} dt \\\ll &\; c^k \int_T^{2T} \bigg| \sum_n \frac{ \beta_L (n) g_x(n)}{ n^{ \lambda_t + it}} - \sum_n \frac{ \beta_L (n) g_x(n)}{ n^{ \sigma_T + it}} \bigg|^{2k} dt \\+&\; c^k \int_T^{2T} ( \lambda_t - \sigma_T )^{2k}\bigg( 1+ ( \lambda_t - \sigma_T ) \log x + \log^+ \frac{1}{ \eta_t \log x } \bigg)^{2k} \\ \times &\;\bigg| \sum_n \frac{ \beta_L (n) g_x(n) \log n }{ n^{ \lambda_t + it}}\bigg|^{2k} dt \\+&\; c^k ( \log T)^{2k} \int_T^{2T} ( \lambda_t - \sigma_T )^{2k}\bigg( 1+ ( \lambda_t - \sigma_T ) \log x + \log^+ \frac{1}{ \eta_t \log x } \bigg)^{2k} dt \\+&\; c^k k^{2k} T e^{- \varepsilon \frac{ \log T}{ G(T)} }\end{split}\end{equation}
for some
![]() $c>0$
. It remains to bound the integrals on the right-hand side.
$c>0$
. It remains to bound the integrals on the right-hand side.
Since
![]() $ k \leq {\varepsilon}/{4} ( \log \log T)^2 $
, we see that
$ k \leq {\varepsilon}/{4} ( \log \log T)^2 $
, we see that
By (2·10) we have
 \begin{equation} \int_T^{2T} \bigg| \sum_n \frac{ \beta_L (n) g_x(n)}{ n^{ \lambda_t + it}} - \sum_n \frac{ \beta_L (n) g_x(n)}{ n^{ \sigma_T + it}} \bigg|^{2k} dt \ll c^k k^{ 2k } T e^{ - \frac{ 1}{4} (\kappa - \frac{3\varepsilon}{k} )\frac{ \log T}{ G(T) } } \frac{ G(T)^k }{ ( \log T)^k } \end{equation}
\begin{equation} \int_T^{2T} \bigg| \sum_n \frac{ \beta_L (n) g_x(n)}{ n^{ \lambda_t + it}} - \sum_n \frac{ \beta_L (n) g_x(n)}{ n^{ \sigma_T + it}} \bigg|^{2k} dt \ll c^k k^{ 2k } T e^{ - \frac{ 1}{4} (\kappa - \frac{3\varepsilon}{k} )\frac{ \log T}{ G(T) } } \frac{ G(T)^k }{ ( \log T)^k } \end{equation}
for some
![]() $ c>0$
. By Lemmas 2·5 and 2·8 we have
$ c>0$
. By Lemmas 2·5 and 2·8 we have
and
 \begin{align*}\int_T^{2T} & ( \lambda_t - \sigma_T)^{2m} \bigg( \log^+ \frac{1}{ \eta_t \log x }\bigg)^{2m} dt \\& \leq \bigg( \int_T^{2T} ( \lambda_t - \sigma_T)^{4m} dt \bigg)^{\frac12} \bigg( \int_T^{2T} \bigg( \log^+ \frac{1}{ \eta_t \log x }\bigg)^{4m}dt \bigg)^{\frac12} \\& \ll \frac{ c^k m^{4m}}{ ( \log T)^{2m}} T e^{ - \frac14 ( \kappa - \frac{ 3\varepsilon}{ k } ) \frac{ \log T}{G(T)} } \end{align*}
\begin{align*}\int_T^{2T} & ( \lambda_t - \sigma_T)^{2m} \bigg( \log^+ \frac{1}{ \eta_t \log x }\bigg)^{2m} dt \\& \leq \bigg( \int_T^{2T} ( \lambda_t - \sigma_T)^{4m} dt \bigg)^{\frac12} \bigg( \int_T^{2T} \bigg( \log^+ \frac{1}{ \eta_t \log x }\bigg)^{4m}dt \bigg)^{\frac12} \\& \ll \frac{ c^k m^{4m}}{ ( \log T)^{2m}} T e^{ - \frac14 ( \kappa - \frac{ 3\varepsilon}{ k } ) \frac{ \log T}{G(T)} } \end{align*}
for
![]() $ k \leq m \leq 4k $
. Thus, we obtain
$ k \leq m \leq 4k $
. Thus, we obtain
 \begin{equation}\begin{split} \int_T^{2T} & ( \lambda_t - \sigma_T )^{2m}\bigg( 1+ ( \lambda_t - \sigma_T ) \log x + \log^+ \frac{1}{ \eta_t \log x } \bigg)^{2m} dt \\ & \ll \frac{ c^k m^{4m}}{ ( \log T)^{2m}} T e^{ - \frac14 ( \kappa - \frac{ 3\varepsilon}{ k } ) \frac{ \log T}{G(T)} } \end{split}\end{equation}
\begin{equation}\begin{split} \int_T^{2T} & ( \lambda_t - \sigma_T )^{2m}\bigg( 1+ ( \lambda_t - \sigma_T ) \log x + \log^+ \frac{1}{ \eta_t \log x } \bigg)^{2m} dt \\ & \ll \frac{ c^k m^{4m}}{ ( \log T)^{2m}} T e^{ - \frac14 ( \kappa - \frac{ 3\varepsilon}{ k } ) \frac{ \log T}{G(T)} } \end{split}\end{equation}
for
![]() $ k \leq m \leq 2k $
. By Lemma 2·6, the Cauchy–Schwarz inequality and the above inequality we have
$ k \leq m \leq 2k $
. By Lemma 2·6, the Cauchy–Schwarz inequality and the above inequality we have
 \begin{equation} \begin{split} \int_T^{2T} & ( \lambda_t - \sigma_T )^{2k}\bigg( 1+ ( \lambda_t - \sigma_T ) \log x + \log^+ \frac{1}{ \eta_t \log x } \bigg)^{2k} \bigg| \sum_n \frac{ \beta_L (n) g_x(n) \log n }{ n^{ \lambda_t + it}}\bigg|^{2k} dt \\ & \ll \frac{ c^k k^{5k} G(T)^{2k} }{ ( \log T)^{2k}} T e^{ - \frac18 ( \kappa - \frac{ 3\varepsilon}{ k } ) \frac{ \log T}{G(T)} } . \end{split} \end{equation}
\begin{equation} \begin{split} \int_T^{2T} & ( \lambda_t - \sigma_T )^{2k}\bigg( 1+ ( \lambda_t - \sigma_T ) \log x + \log^+ \frac{1}{ \eta_t \log x } \bigg)^{2k} \bigg| \sum_n \frac{ \beta_L (n) g_x(n) \log n }{ n^{ \lambda_t + it}}\bigg|^{2k} dt \\ & \ll \frac{ c^k k^{5k} G(T)^{2k} }{ ( \log T)^{2k}} T e^{ - \frac18 ( \kappa - \frac{ 3\varepsilon}{ k } ) \frac{ \log T}{G(T)} } . \end{split} \end{equation}
Therefore, by (2·17) – (2·20) there exist
![]() $ \kappa_0 >0 $
such that
$ \kappa_0 >0 $
such that
 \begin{equation}\int_T^{2T} \bigg| \log L ( \sigma_T + it ) - \sum_{ n} \frac{ \beta_L (n) g_x (n) }{ n^{ \sigma_T + it }} \bigg|^{2k} dt \ll c^k k^{4k} T e^{ - \kappa_0 \frac{ \log T}{G(T)} }.\end{equation}
\begin{equation}\int_T^{2T} \bigg| \log L ( \sigma_T + it ) - \sum_{ n} \frac{ \beta_L (n) g_x (n) }{ n^{ \sigma_T + it }} \bigg|^{2k} dt \ll c^k k^{4k} T e^{ - \kappa_0 \frac{ \log T}{G(T)} }.\end{equation}
Let
![]() $ k=1$
in (2·21), then we see that
$ k=1$
in (2·21), then we see that
where
![]() $ x = T^\varepsilon$
and
$ x = T^\varepsilon$
and
![]() $ 0< \varepsilon < \min\{ {1}/{48}, {\kappa}/3 \} $
. Let
$ 0< \varepsilon < \min\{ {1}/{48}, {\kappa}/3 \} $
. Let
![]() $ e^{ \frac{G(T)}{2}} \leq Y \leq x $
, then we have
$ e^{ \frac{G(T)}{2}} \leq Y \leq x $
, then we have
 \begin{equation} \int_T^{2T} \bigg| \sum_{ n>Y } \frac{ \beta_L (n) g_x (n) }{ n^{ \sigma_T + it }} \bigg|^{2} dt \ll T \sum_{ n >Y } \frac{ | \beta_L (n) |^2 }{ n^{2 \sigma_T }} \ll T \frac{Y^{1-2\sigma_T} }{ (2 \sigma_T - 1 ) \log Y } \end{equation}
\begin{equation} \int_T^{2T} \bigg| \sum_{ n>Y } \frac{ \beta_L (n) g_x (n) }{ n^{ \sigma_T + it }} \bigg|^{2} dt \ll T \sum_{ n >Y } \frac{ | \beta_L (n) |^2 }{ n^{2 \sigma_T }} \ll T \frac{Y^{1-2\sigma_T} }{ (2 \sigma_T - 1 ) \log Y } \end{equation}
by [ Reference Lamzouri and Lee4 , lemma 4·1]. Thus, Theorem 2·1 follows from (2·22) and (2·23).
Next we prove Theorem 2·2. We see that (2·2) holds by (2·9) and (2·21). The proof of (2·3) is similar, but simpler than the proof of Lemma 2·6. Since
 \begin{align*} \log L( \sigma_T, \mathbb{X} ) = & \sum_{ p } \frac{ \beta_L (p) \mathbb{X} (p) }{ p^{ \sigma_T }}+\sum_{ p } \frac{ \beta_L (p^2 ) \mathbb{X} (p^2 ) }{ p^{ 2\sigma_T } } +O(1), \end{align*}
\begin{align*} \log L( \sigma_T, \mathbb{X} ) = & \sum_{ p } \frac{ \beta_L (p) \mathbb{X} (p) }{ p^{ \sigma_T }}+\sum_{ p } \frac{ \beta_L (p^2 ) \mathbb{X} (p^2 ) }{ p^{ 2\sigma_T } } +O(1), \end{align*}
by [ Reference Tsang16 , lemma 3·3] we have
 \begin{align*}\mathbb E[ | \log L( \sigma_T, \mathbb{X} )|^{2k} ] \leq & c^k \bigg( k! \bigg( \sum_{ p } \frac{ | \beta_L (p) |^2 }{ p^{ 2\sigma_T }} \bigg)^k + k! \bigg( \sum_{ p } \frac{ | \beta_L (p^2 )|^2 }{ p^{ 4\sigma_T } } \bigg)^k + 1 \bigg) \end{align*}
\begin{align*}\mathbb E[ | \log L( \sigma_T, \mathbb{X} )|^{2k} ] \leq & c^k \bigg( k! \bigg( \sum_{ p } \frac{ | \beta_L (p) |^2 }{ p^{ 2\sigma_T }} \bigg)^k + k! \bigg( \sum_{ p } \frac{ | \beta_L (p^2 )|^2 }{ p^{ 4\sigma_T } } \bigg)^k + 1 \bigg) \end{align*}
for some
![]() $ c > 0 $
. By (2·7) and assumption A4 we have
$ c > 0 $
. By (2·7) and assumption A4 we have
 \begin{align*}\sum_{ p } \frac{ |\beta_L (p^2) |^2 }{ p^{ 4 \sigma_T }} \ll \sum_{ p } \frac{ \sum_{i=1}^d |\alpha_i (p ) |^2 }{ p^{ 2-2 \eta }} \ll 1.\end{align*}
\begin{align*}\sum_{ p } \frac{ |\beta_L (p^2) |^2 }{ p^{ 4 \sigma_T }} \ll \sum_{ p } \frac{ \sum_{i=1}^d |\alpha_i (p ) |^2 }{ p^{ 2-2 \eta }} \ll 1.\end{align*}
By assumption A6 we have
 \begin{align*} \sum_{ p } \frac{ |\beta_L (p) |^2 }{ p^{2 \sigma_T} } \ll \int_2^\infty \frac{ du}{ u^{1+ \frac{2}{ G(T)}} \log u } \ll \log G(T).\end{align*}
\begin{align*} \sum_{ p } \frac{ |\beta_L (p) |^2 }{ p^{2 \sigma_T} } \ll \int_2^\infty \frac{ du}{ u^{1+ \frac{2}{ G(T)}} \log u } \ll \log G(T).\end{align*}
Thus, we have
for some
![]() $ c >0$
.
$ c >0$
.
3. Discrepancy
In this section we will prove Theorem 1·2 for G(T) satisfying (2·1). First we need to extend [
Reference Lamzouri and Lee4
, proposition 5·1]. Define the Fourier transforms of
![]() $\Phi_T $
and
$\Phi_T $
and
![]() $ \Phi_T^{\textrm{rand}} $
by
$ \Phi_T^{\textrm{rand}} $
by
and
where
![]() $ \mathbf{x} = ( x_1, \ldots, x_J ) $
and similarly
$ \mathbf{x} = ( x_1, \ldots, x_J ) $
and similarly
![]() $ \mathbf{y}, \mathbf{u}, \mathbf{v}$
are vectors in
$ \mathbf{y}, \mathbf{u}, \mathbf{v}$
are vectors in
![]() $ \mathbb{R}^J$
and
$ \mathbb{R}^J$
and
![]() $ \mathbf{x} \cdot \mathbf{u} \;:\!=\; \sum_{ j \leq J } x_j u_j $
is the dot product. Then we obtain the following proposition.
$ \mathbf{x} \cdot \mathbf{u} \;:\!=\; \sum_{ j \leq J } x_j u_j $
is the dot product. Then we obtain the following proposition.
Proposition 3·1. Assume (2·1). Given constant
![]() $A_4>0$
, there exists a constant
$A_4>0$
, there exists a constant
![]() $ A_5 >0$
such that
$ A_5 >0$
such that
for
![]() $\max_{ j \leq J} \{ |x_j |, |y_j | \} \leq { \sqrt{ \log T}}/{ A_5 \sqrt{ G(T)} \log \log T} $
.
$\max_{ j \leq J} \{ |x_j |, |y_j | \} \leq { \sqrt{ \log T}}/{ A_5 \sqrt{ G(T)} \log \log T} $
.
Proof. By definition we get
 \begin{align*} \widehat{\Phi}_T( \mathbf{x}, \mathbf{y} ) & = \frac1T \int_T^{2T} \exp \bigg[ 2 \pi i \sum_{ j \leq J} \big( x_j \log | L_j ( \sigma_T + it ) | + y_j \arg L_j ( \sigma_T + i t ) \big) \bigg] dt, \\ \widehat{\Phi}_T^{\textrm{rand}}( \mathbf{x}, \mathbf{y}) & = \mathbb{E} \bigg[ \exp \bigg[ 2 \pi i \sum_{ j \leq J} \big( x_j \log | L_j ( \sigma_T, X ) | + y_j \arg L_j ( \sigma_T, \mathbb{X} ) \big) \bigg] \bigg]. \end{align*}
\begin{align*} \widehat{\Phi}_T( \mathbf{x}, \mathbf{y} ) & = \frac1T \int_T^{2T} \exp \bigg[ 2 \pi i \sum_{ j \leq J} \big( x_j \log | L_j ( \sigma_T + it ) | + y_j \arg L_j ( \sigma_T + i t ) \big) \bigg] dt, \\ \widehat{\Phi}_T^{\textrm{rand}}( \mathbf{x}, \mathbf{y}) & = \mathbb{E} \bigg[ \exp \bigg[ 2 \pi i \sum_{ j \leq J} \big( x_j \log | L_j ( \sigma_T, X ) | + y_j \arg L_j ( \sigma_T, \mathbb{X} ) \big) \bigg] \bigg]. \end{align*}
Since the inequality
holds for any
![]() $ x,y \in \mathbb{R} $
, by the Cauchy–Schwarz inequality and Theorem 2·1 with
$ x,y \in \mathbb{R} $
, by the Cauchy–Schwarz inequality and Theorem 2·1 with
we have
 \begin{align*} \widehat{\Phi}_T( \mathbf{x}, \mathbf{y} ) & - \frac1T \int_T^{2T} \exp \bigg[ 2 \pi i \sum_{ j \leq J} \big( x_j \text{Re} ( R_{j, Y} ( \sigma_T + it )) + y_j \text{Im} ( R_{j,Y} ( \sigma_T + i t ) ) \big) \bigg] dt \\ = &\; O \bigg( \frac1T \int_T^{2T} \sum_{j \leq J} ( |x_j| + |y_j | ) | \log L_j ( \sigma_T + it ) - R_{j,Y} ( \sigma_T + it ) | dt \bigg) \\ = &\; O \bigg( \sum_{j \leq J} ( |x_j| + |y_j | ) \bigg( \frac1T \int_T^{2T} | \log L_j ( \sigma_T + it ) - R_{j,Y} ( \sigma_T + it ) |^2 dt \bigg)^{ \frac12} \bigg) \\ = &\; O \bigg( \frac{ M }{ ( \log T)^{A_6}} \bigg)\end{align*}
\begin{align*} \widehat{\Phi}_T( \mathbf{x}, \mathbf{y} ) & - \frac1T \int_T^{2T} \exp \bigg[ 2 \pi i \sum_{ j \leq J} \big( x_j \text{Re} ( R_{j, Y} ( \sigma_T + it )) + y_j \text{Im} ( R_{j,Y} ( \sigma_T + i t ) ) \big) \bigg] dt \\ = &\; O \bigg( \frac1T \int_T^{2T} \sum_{j \leq J} ( |x_j| + |y_j | ) | \log L_j ( \sigma_T + it ) - R_{j,Y} ( \sigma_T + it ) | dt \bigg) \\ = &\; O \bigg( \sum_{j \leq J} ( |x_j| + |y_j | ) \bigg( \frac1T \int_T^{2T} | \log L_j ( \sigma_T + it ) - R_{j,Y} ( \sigma_T + it ) |^2 dt \bigg)^{ \frac12} \bigg) \\ = &\; O \bigg( \frac{ M }{ ( \log T)^{A_6}} \bigg)\end{align*}
for all
![]() $ |x_j |, |y_j | \leq M$
. Let
$ |x_j |, |y_j | \leq M$
. Let
then by the Taylor theorem and [ Reference Lamzouri and Lee4 , lemma 4·5] we have
 \begin{align*} \widehat{\Phi}_T( \mathbf{x}, \mathbf{y} ) - & \sum_{n=0}^{2N-1} \frac{ (2 \pi i)^n }{ n! T } \int_T^{2T} \bigg( \sum_{ j \leq J} \big( x_j \text{Re} ( R_{j, Y} ( \sigma_T + it )) + y_j \text{Im} ( R_{j,Y} ( \sigma_T + i t ) ) \big) \bigg)^n dt \\= &\; O \bigg( \frac{ c^N M^{2N} }{(2N)! } \frac1T \int_T^{2T} \sum_{ j \leq J} \big| R_{j,Y} ( \sigma_T + i t ) \big|^{2N} dt + \frac{ M }{( \log T)^{A_6}} \bigg)\\ = & \; O \bigg( \bigg( \frac{ c M^2 \log \log T}{N} \bigg)^N + \frac{ M }{( \log T)^{A_6}} \bigg)\end{align*}
\begin{align*} \widehat{\Phi}_T( \mathbf{x}, \mathbf{y} ) - & \sum_{n=0}^{2N-1} \frac{ (2 \pi i)^n }{ n! T } \int_T^{2T} \bigg( \sum_{ j \leq J} \big( x_j \text{Re} ( R_{j, Y} ( \sigma_T + it )) + y_j \text{Im} ( R_{j,Y} ( \sigma_T + i t ) ) \big) \bigg)^n dt \\= &\; O \bigg( \frac{ c^N M^{2N} }{(2N)! } \frac1T \int_T^{2T} \sum_{ j \leq J} \big| R_{j,Y} ( \sigma_T + i t ) \big|^{2N} dt + \frac{ M }{( \log T)^{A_6}} \bigg)\\ = & \; O \bigg( \bigg( \frac{ c M^2 \log \log T}{N} \bigg)^N + \frac{ M }{( \log T)^{A_6}} \bigg)\end{align*}
for some
![]() $ c>0$
. Let
$ c>0$
. Let
with a constant
![]() $A_5 \geq \sqrt{ 10 c A_6 }e^{ 5A_6^2} $
, then we have
$A_5 \geq \sqrt{ 10 c A_6 }e^{ 5A_6^2} $
, then we have
 \begin{align*} \widehat{\Phi}_T( \mathbf{x}, \mathbf{y} ) = & \sum_{n=0}^{2N-1} \frac{ (2 \pi i)^n }{ n! T } \int_T^{2T} \bigg( \sum_{ j \leq J} \big( x_j \text{Re} ( R_{j, Y} ( \sigma_T + it )) + y_j \text{Im} ( R_{j,Y} ( \sigma_T + i t ) ) \big) \bigg)^n dt \\ & \; + O \bigg( \frac{ 1 }{( \log T)^{A_6 - \frac12}} \bigg) .\end{align*}
\begin{align*} \widehat{\Phi}_T( \mathbf{x}, \mathbf{y} ) = & \sum_{n=0}^{2N-1} \frac{ (2 \pi i)^n }{ n! T } \int_T^{2T} \bigg( \sum_{ j \leq J} \big( x_j \text{Re} ( R_{j, Y} ( \sigma_T + it )) + y_j \text{Im} ( R_{j,Y} ( \sigma_T + i t ) ) \big) \bigg)^n dt \\ & \; + O \bigg( \frac{ 1 }{( \log T)^{A_6 - \frac12}} \bigg) .\end{align*}
By following the second half of the proof of [ Reference Lamzouri and Lee4 , proposition 5·1] one can conclude that the proposition holds.
We next need to introduce Beurling–Selberg functions. Define
for
![]() $ z\in \mathbb{C}$
and
$ z\in \mathbb{C}$
and
![]() $ \Delta > 0$
, where
$ \Delta > 0$
, where
 \begin{align*} H(z) = \frac{ \sin^2 (\pi z) }{ \pi^2 } \bigg( \sum_{n=-\infty}^\infty \frac{ \textrm{sgn} (n) }{(z-n)^2 } + \frac{2}{z} \bigg) \quad \textrm{and} \quad K(z) = \frac{ \sin^2 (\pi z) }{ ( \pi z)^2}. \end{align*}
\begin{align*} H(z) = \frac{ \sin^2 (\pi z) }{ \pi^2 } \bigg( \sum_{n=-\infty}^\infty \frac{ \textrm{sgn} (n) }{(z-n)^2 } + \frac{2}{z} \bigg) \quad \textrm{and} \quad K(z) = \frac{ \sin^2 (\pi z) }{ ( \pi z)^2}. \end{align*}
Then we summarise some results in [ Reference Lamzouri, Lester and Radziwiłł6 , section 7] as a lemma.
Lemma 3·2. For all
![]() $x \in \mathbb{R}$
we have
$x \in \mathbb{R}$
we have
![]() $| F_{ [a,b], \Delta} (x) | \leq 1 $
and
$| F_{ [a,b], \Delta} (x) | \leq 1 $
and
Moreover, the Fourier transform
![]() $ \widehat{F}_{ [a,b], \Delta} $
satisfies
$ \widehat{F}_{ [a,b], \Delta} $
satisfies
 \begin{align*} \widehat{F}_{ [a,b], \Delta} = \begin{cases}\widehat{\mathbf{1}}_{[a,b] }(y) + O ( \Delta^{-1}) & \textrm{if} \; |y| \leq \Delta, \\0 & \textrm{if}\; |y| \geq \Delta.\end{cases}\end{align*}
\begin{align*} \widehat{F}_{ [a,b], \Delta} = \begin{cases}\widehat{\mathbf{1}}_{[a,b] }(y) + O ( \Delta^{-1}) & \textrm{if} \; |y| \leq \Delta, \\0 & \textrm{if}\; |y| \geq \Delta.\end{cases}\end{align*}
We are ready to prove Theorem 1·2 for G(T) satisfying (2·1). By Corollary 2·3 there exists a constant
![]() $A_3>0$
such that
$A_3>0$
such that
 \begin{align*} \frac{1}{T} \text{meas} \{ t \in [T, 2T] : \mathbf{L} ( \sigma_T + it ) \notin I_T \} & \ll \frac{1}{ ( \log T)^{10}}, \\ \mathbb P \{ \mathbf{L} ( \sigma_T, \mathbb{X} ) \notin I_T \} & \ll \frac{1}{ ( \log T)^{10}},\end{align*}
\begin{align*} \frac{1}{T} \text{meas} \{ t \in [T, 2T] : \mathbf{L} ( \sigma_T + it ) \notin I_T \} & \ll \frac{1}{ ( \log T)^{10}}, \\ \mathbb P \{ \mathbf{L} ( \sigma_T, \mathbb{X} ) \notin I_T \} & \ll \frac{1}{ ( \log T)^{10}},\end{align*}
where
Then we see that
 \begin{align*} \Phi_T( \mathcal R) & = \Phi_T ( \mathcal R \cap I_T ) + O \bigg( \frac{1}{ ( \log T)^{10}} \bigg), \\ \Phi_T^{\textrm{rand}} ( \mathcal R) & = \Phi_T^{\textrm{rand}} ( \mathcal R \cap I_T ) + O \bigg( \frac{1}{ ( \log T)^{10}} \bigg) \end{align*}
\begin{align*} \Phi_T( \mathcal R) & = \Phi_T ( \mathcal R \cap I_T ) + O \bigg( \frac{1}{ ( \log T)^{10}} \bigg), \\ \Phi_T^{\textrm{rand}} ( \mathcal R) & = \Phi_T^{\textrm{rand}} ( \mathcal R \cap I_T ) + O \bigg( \frac{1}{ ( \log T)^{10}} \bigg) \end{align*}
for any
![]() $\mathcal R \in \mathbb{R}^{2J}$
. Thus, we have
$\mathcal R \in \mathbb{R}^{2J}$
. Thus, we have
where
![]() $\mathcal R \subset I_T $
runs over all rectangular boxes of
$\mathcal R \subset I_T $
runs over all rectangular boxes of
![]() $ \mathbb{R}^{2J}$
with sides parallel to the coordinate axes. By (3·1) it is enough to show that
$ \mathbb{R}^{2J}$
with sides parallel to the coordinate axes. By (3·1) it is enough to show that
for
 \begin{align*} \mathcal R = \prod_{j=1}^J I_{1,j} \times \prod_{j=1}^J I_{2,j} \subset I_T , \end{align*}
\begin{align*} \mathcal R = \prod_{j=1}^J I_{1,j} \times \prod_{j=1}^J I_{2,j} \subset I_T , \end{align*}
where
![]() $I_{1,j} = [a_j, b_j ]$
and
$I_{1,j} = [a_j, b_j ]$
and
![]() $ I_{2,j} = [c_j, d_j ] $
for
$ I_{2,j} = [c_j, d_j ] $
for
![]() $ j = 1, \ldots, J$
.
$ j = 1, \ldots, J$
.
By definition we see that
 \begin{align*} \Phi_T ( \mathcal R) & = \frac{1}{T} \int_T^{2T} \prod_{j=1}^J \mathbf{1}_{ I_{1,j} } ( \log | L_j ( \sigma_T + i t )| ) \mathbf{1}_{ I_{2,j} } ( \arg L_j ( \sigma_T + i t ) ) dt , \\ \Phi_T^{\textrm{rand}} (\mathcal R) & = \mathbb E \bigg[ \prod_{j=1}^J \mathbf{1}_{ I_{1,j} } ( \log | L_j ( \sigma_T, \mathbb{X} )| ) \mathbf{1}_{ I_{2,j} } ( \arg L_j ( \sigma_T, \mathbb{X}) ) \bigg] . \end{align*}
\begin{align*} \Phi_T ( \mathcal R) & = \frac{1}{T} \int_T^{2T} \prod_{j=1}^J \mathbf{1}_{ I_{1,j} } ( \log | L_j ( \sigma_T + i t )| ) \mathbf{1}_{ I_{2,j} } ( \arg L_j ( \sigma_T + i t ) ) dt , \\ \Phi_T^{\textrm{rand}} (\mathcal R) & = \mathbb E \bigg[ \prod_{j=1}^J \mathbf{1}_{ I_{1,j} } ( \log | L_j ( \sigma_T, \mathbb{X} )| ) \mathbf{1}_{ I_{2,j} } ( \arg L_j ( \sigma_T, \mathbb{X}) ) \bigg] . \end{align*}
By Lemma 3·2 with
![]() $\Delta = M$
we have
$\Delta = M$
we have
 \begin{equation}\begin{split} \Phi_T ( \mathcal R) & = \frac{1}{T} \int_T^{2T} \prod_{j=1}^J F_{ I_{1,j}, M} ( \log | L_j ( \sigma_T + i t )| ) F_{ I_{2,j}, M } ( \arg L_j ( \sigma_T + i t ) ) dt + O( M^{-1} ) , \\ \Phi_T^{\textrm{rand}} (\mathcal R) & = \mathbb E \bigg[ \prod_{j=1}^J F_{ I_{1,j}, M} ( \log | L_j ( \sigma_T, \mathbb{X} )| ) F_{ I_{2,j}, M} ( \arg L_j ( \sigma_T, \mathbb{X}) ) \bigg] + O( M^{-1} ) . \end{split}\end{equation}
\begin{equation}\begin{split} \Phi_T ( \mathcal R) & = \frac{1}{T} \int_T^{2T} \prod_{j=1}^J F_{ I_{1,j}, M} ( \log | L_j ( \sigma_T + i t )| ) F_{ I_{2,j}, M } ( \arg L_j ( \sigma_T + i t ) ) dt + O( M^{-1} ) , \\ \Phi_T^{\textrm{rand}} (\mathcal R) & = \mathbb E \bigg[ \prod_{j=1}^J F_{ I_{1,j}, M} ( \log | L_j ( \sigma_T, \mathbb{X} )| ) F_{ I_{2,j}, M} ( \arg L_j ( \sigma_T, \mathbb{X}) ) \bigg] + O( M^{-1} ) . \end{split}\end{equation}
To confirm the above O-terms, it requires inequalities similar to
 \begin{align*} \frac{1}{T} \int_T^{2T} & K( M ( \log |L_1 ( \sigma_T + it ) | - \alpha) ) dt \\ & = \frac{1}{M} \int_{-M}^M \bigg( 1 - \frac{ |u|}{M} \bigg) e^{- 2 \pi i \alpha u } \widehat{\Phi}_T ( u, 0, \ldots, 0 ) du \ll \frac{1}{M},\end{align*}
\begin{align*} \frac{1}{T} \int_T^{2T} & K( M ( \log |L_1 ( \sigma_T + it ) | - \alpha) ) dt \\ & = \frac{1}{M} \int_{-M}^M \bigg( 1 - \frac{ |u|}{M} \bigg) e^{- 2 \pi i \alpha u } \widehat{\Phi}_T ( u, 0, \ldots, 0 ) du \ll \frac{1}{M},\end{align*}
which holds by Fourier inversion, Proposition 3·1, [ Reference Lamzouri and Lee4 , lemma 7·1] and
By Fourier inversion, Lemma 3·2 and Proposition 3·1 we obtain
 \begin{equation}\begin{split}& \frac{1}{T} \int_T^{2T} \prod_{j=1}^J F_{ I_{1,j}, M} ( \log | L_j ( \sigma_T + i t )| ) F_{ I_{2,j}, M } ( \arg L_j ( \sigma_T + i t ) ) dt \\& = \int_{ \mathbb{R}^{2J}} \bigg( \prod_{j=1}^J \widehat{F}_{ I_{1,j}, M} (x_j) \widehat{F}_{ I_{2,j}, M} (y_j) \bigg) \widehat{\Phi}_T (\!-\! \mathbf{x}, - \mathbf{y} ) d \mathbf{x} d \mathbf{y} \\& = \int_{ \substack{ |x_j|, |y_j | \leq M \\ j = 1, \ldots, J } } \bigg( \prod_{j=1}^J \widehat{F}_{ I_{1,j}, M} (x_j) \widehat{F}_{ I_{2,j}, M} (y_j) \bigg) \widehat{\Phi}_T^{\textrm{rand}} (\!-\! \mathbf{x}, - \mathbf{y} ) d \mathbf{x} d \mathbf{y} + O\bigg( \frac{( M \log \log T )^{2J}}{( \log T)^{A_4}} \bigg) \\&= \mathbb E \bigg[ \prod_{j=1}^J F_{ I_{1,j}, M} ( \log | L_j ( \sigma_T, \mathbb{X} )| ) F_{ I_{2,j}, M} ( \arg L_j ( \sigma_T, \mathbb{X}) ) \bigg] + O\bigg( \frac{( M \log \log T )^{2J}}{( \log T)^{A_4}} \bigg) . \end{split}\end{equation}
\begin{equation}\begin{split}& \frac{1}{T} \int_T^{2T} \prod_{j=1}^J F_{ I_{1,j}, M} ( \log | L_j ( \sigma_T + i t )| ) F_{ I_{2,j}, M } ( \arg L_j ( \sigma_T + i t ) ) dt \\& = \int_{ \mathbb{R}^{2J}} \bigg( \prod_{j=1}^J \widehat{F}_{ I_{1,j}, M} (x_j) \widehat{F}_{ I_{2,j}, M} (y_j) \bigg) \widehat{\Phi}_T (\!-\! \mathbf{x}, - \mathbf{y} ) d \mathbf{x} d \mathbf{y} \\& = \int_{ \substack{ |x_j|, |y_j | \leq M \\ j = 1, \ldots, J } } \bigg( \prod_{j=1}^J \widehat{F}_{ I_{1,j}, M} (x_j) \widehat{F}_{ I_{2,j}, M} (y_j) \bigg) \widehat{\Phi}_T^{\textrm{rand}} (\!-\! \mathbf{x}, - \mathbf{y} ) d \mathbf{x} d \mathbf{y} + O\bigg( \frac{( M \log \log T )^{2J}}{( \log T)^{A_4}} \bigg) \\&= \mathbb E \bigg[ \prod_{j=1}^J F_{ I_{1,j}, M} ( \log | L_j ( \sigma_T, \mathbb{X} )| ) F_{ I_{2,j}, M} ( \arg L_j ( \sigma_T, \mathbb{X}) ) \bigg] + O\bigg( \frac{( M \log \log T )^{2J}}{( \log T)^{A_4}} \bigg) . \end{split}\end{equation}
Here, we also have used that
for
![]() $ |y| \leq M $
and
$ |y| \leq M $
and
![]() $ | b-a | \ll \log \log T $
. We choose
$ | b-a | \ll \log \log T $
. We choose
![]() $A_4 $
sufficiently large so that
$A_4 $
sufficiently large so that
then (3·2) holds by (3·3) and (3·4). This completes the proof of Theorem 1·2.
Acknowledgements
This work has been supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIP) (No. 2019R1F1A1050795).