Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-15T01:18:13.515Z Has data issue: false hasContentIssue false
  • English
  • Français

Embeddings in Euclidean space

Published online by Cambridge University Press:  24 October 2008

R. L. E. Schwarzenberger
R. L. E. Schwarzenberger
Affiliation:
Department of Pure Mathematics, University of Liverpool
Get access Rights & Permissions [Opens in a new window]

Extract

Let X be a compact differentiable manifold without boundary. A differentiable regular map of X into Euclidean N-space, dim X < N, is called an immersion (written X £ N). An immersion which is also one-one is called an embedding (written X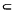N). A nonembedding theorem of the form: if X is a manifold with the property P then X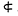N − 1, is best possible if there exists a manifold X with property P and an embedding X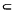N. The purpose of this note is to show that two frequently used non-embedding theorems are best possible.

Type
Research Notes
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 59 , Issue 2 , April 1963 , pp. 505 - 507
Copyright
Copyright © Cambridge Philosophical Society 1963

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Atiyah, M. F. and Hirzebruch, F.Quelques théorèmes de non-plongement pour les variétés differentiables. Bull. Soc. Math. France, 87 (1959), 383–396.Google Scholar
(2)Epstein, D. B. A. and Schwarzenberger, R. L. E., Imbeddings of real projective spaces. Ann. of Math. 76 (1962), 180–184.CrossRefGoogle Scholar
(3)Massey, W. S., On the Stiefel-Whitney classes of a manifold. Amer. J. Math. 82 (1960), 92–102.CrossRefGoogle Scholar
(4)Sanderson, B. J., Immersions and embeddings of projective spaces. Proc. London Math. Soc. (in the press).Google Scholar