Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Beardsley, Jonathan
and
Morava, Jack
2018.
Toward a Galois theory of the integers over the sphere spectrum.
Journal of Geometry and Physics,
Vol. 131,
Issue. ,
p.
41.
Balmer, Paul
Krause, Henning
and
Stevenson, Greg
2019.
Tensor-triangular fields: ruminations.
Selecta Mathematica,
Vol. 25,
Issue. 1,
Balmer, Paul
2020.
Homological support of big objects in tensor-triangulated categories.
Journal de l’École polytechnique — Mathématiques,
Vol. 7,
Issue. ,
p.
1069.
Barbieri-Viale, Luca
Huber, Annette
and
Prest, Mike
2020.
Tensor structure for Nori motives.
Pacific Journal of Mathematics,
Vol. 306,
Issue. 1,
p.
1.
Balmer, Paul
2020.
Nilpotence theorems via homological residue fields.
Tunisian Journal of Mathematics,
Vol. 2,
Issue. 2,
p.
359.
Verasdanis, Charalampos
2023.
Stratification and the smashing spectrum.
Mathematische Zeitschrift,
Vol. 305,
Issue. 4,
Barthel, Tobias
Castellana, Natàlia
Heard, Drew
Naumann, Niko
Pol, Luca
and
Sanders, Beren
2024.
Triangulated Categories in Representation Theory and Beyond.
Vol. 17,
Issue. ,
p.
1.
Prest, Mike
and
Wagstaffe, Rose
2024.
Model theory in compactly generated (tensor-)triangulated categories.
Model Theory,
Vol. 3,
Issue. 1,
p.
147.
Balchin, Scott
and
Tecklenburg, Florian
2025.
Classifying smashing ideals in derived categories of valuation domains.
Journal of Pure and Applied Algebra,
Vol. 229,
Issue. 3,
p.
107917.
Bird, Isaac
and
Williamson, Jordan
2025.
The homological spectrum via definable subcategories.
Bulletin of the London Mathematical Society,


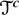 of a tensor-triangulated category
of a tensor-triangulated category 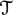 comes from a unique smashing ideal in
comes from a unique smashing ideal in 