No CrossRef data available.
Published online by Cambridge University Press: 24 October 2008
Although integrable Hamiltonian systems are non-generic (Robinson (13)) they have some importance in classical mechanics, e.g. the two-body problem, a free rigid body not subject to a gravitational field, the Toda lattice (Moser(12)). Arnol'd (cf. (2) and (1), appendix 26) proved that under quite general conditions action-angle coordinates can be introduced. Accordingly we consider a fixed system 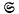 with n degrees of freedom in the standard form
with n degrees of freedom in the standard form
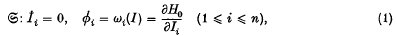
where H0 is a smooth function of the action variables Li only and I ∈ I and I is an open set of n-tuples of positive reals. 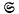 now subjected to a periodic impressed force, the resulting system,
now subjected to a periodic impressed force, the resulting system, 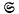 , being determined by a small, periodic perturbation of the energy function
, being determined by a small, periodic perturbation of the energy function
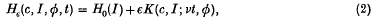
where e is a small positive real and K(c, I; α0, α1, …, an) is a smooth function of parameters c ranging over a smooth r-manifold E, I ∈ I, and K has period 2π in each of the angles αi, i.e. (α0, …, αn) ∈ Tn (n-torus). The purpose of this paper is to define the forms of bifurcation of oscillations of the perturbed system 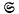 (K):
(K):