Gradient configurations and quadratic functions

Extract

A normal preference system for a combination of goods is represented by an increasing function φ with convex levels. From Gossen's law, that preference and price directions coincide in equilibrium (a special consequence of his Second Law), it follows that, on the data that x_r is the vector of quantities purchased at prices given by a vector p_r (r = 1,…, k), the gradient g_r = g(x_r) of the function φ at the point x_r is given by

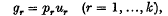
for some positive multiplier μ_r;. There may be considered the class of preference functions thus satisfying Gossen's law in respect to the data, and thus with gradients taking prescribed directions at k prescribed points. In particular, there may be considered the subclass of these which are quadratic in some convex region containing the points x_r. By choosing any multipliers μ_r, there is obtained a set of gradients g_r associated with the points x_r. It is asked if there exists a quadratic function which is increasing and has convex levels in a convex neighbourhood of the points x_r, and whose gradient at x_r is g_r; also it is required to characterize the class of such functions, which, if any exist, form an infinite variety. This is the background of the questions which are going to be investigated, and which are of importance in a general method of empirical preference analysis in economics.