Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T16:08:21.312Z Has data issue: false hasContentIssue false
  • English
  • Français

Images of fractional Brownian motion with deterministic drift: Positive Lebesgue measure and non-empty interior

Part of: Markov processes

Published online by Cambridge University Press:  28 February 2022

MOHAMED ERRAOUI  and
YOUSSEF HAKIKI
MOHAMED ERRAOUI
Affiliation:
Faculty of Sciences, Route Ben Maachou, B.P. 20, 24000, El Jadida, Morocco. e-mail: erraoui@uca.ac.ma
YOUSSEF HAKIKI
Affiliation:
Faculty of Science Semlalia, Bd. Prince My Abdellah, B.P. 2390, 40000, Marrakech, Morocco. e-mail: youssef.hakiki@ced.uca.ma
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 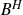$B^{H}$ be a fractional Brownian motion in 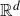$\mathbb{R}^{d}$ of Hurst index 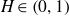$H\in\left(0,1\right)$ , $f\;:\;\left[0,1\right]\longrightarrow\mathbb{R}^{d}$ a Borel function and 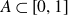$A\subset\left[0,1\right]$ a Borel set. We provide sufficient conditions for the image 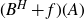$(B^{H}+f)(A)$ to have a positive Lebesgue measure or to have a non-empty interior. This is done through the study of the properties of the density of the occupation measure of 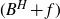$(B^{H}+f)$ . Precisely, we prove that if the parabolic Hausdorff dimension of the graph of f is greater than Hd, then the density is a square integrable function. If, on the other hand, the Hausdorff dimension of A is greater than Hd, then it even admits a continuous version. This allows us to establish the result already cited.

MSC classification

Primary: 60J65: Brownian motion
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 173 , Issue 3 , November 2022 , pp. 693 - 713
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adler, R. J.. The Geometry of Random Fields (Wiley, 1981).Google Scholar
Antunović, T., Peres, Y. and Vermesi, B.. Brownian motion with variable drift can be space filling. Proc. Amer. Math. Soc. 139, no. 9 (2011), 3359-3373.CrossRefGoogle Scholar
Balança, P.. Some sample path properties of multifractional Brownian motion. Stochastic Process. Appl. 125, no. 10 (2015), 3823-3850.CrossRefGoogle Scholar
Bishop, C. J. and Peres, Y.. Fractals in probability and analysis. Camb. Stud. Adv. Math. 162. (Cambridge University Press, 2017).CrossRefGoogle Scholar
Cuzick, J. and DuPreez, J. P.. Joint continuity of Gaussian local times. Ann. Probab. 10, no. 3 (1982), 810–817.Google Scholar
Falconer, K. J.. Fractal geometry-mathematical foundations and applications (John Wiley and Sons, 1990).CrossRefGoogle Scholar
Geman, D. and Horowitz, J.. Occupation densities. Ann. Probab. 8, no. 1 (1980), 1-67.CrossRefGoogle Scholar
Geman, D., Horowitz, J. and Rosen, J. A local time analysis of intersections of Brownian motion in the plane. Ann. Probab. 12 (1984), 86–107.CrossRefGoogle Scholar
Graversen, S. E.. Polar-functions for Brownian motion. Z. Wahrsch. Verw. Gebiete 61, no. 2 (1982), 261-270.CrossRefGoogle Scholar
Kahane, J. P.. Some Random Series of Functions (Cambridge University Press, 1985).Google Scholar
Kaufman, R.. Une propriété métrique du mouvement brownien. C. R. Acad. Sci. Paris Sér. A-B 268 (1969), A727-A728.Google Scholar
Khoshnevisan, D.. Multiparameter Processes. An Introduction to Random Fields. (Springer-Verlag, 2002).Google Scholar
Khoshnevisan, D. and Xiao, Y.. Brownian motion and thermal capacity. Ann. Probab. 43, no. 1 (2015), 405-434.CrossRefGoogle Scholar
Le Gall, J. F.. Sur les fonctions polaires pour le mouvement brownien. Séminaire de Probabilités, XXII. Lecture Notes in Math. vol. 1321 (Springer, Berlin, 1988), 186-189.Google Scholar
Mattila, P. Geometry of sets and measures in Euclidean spaces. Fractals and rectifiability. Camb. Stud. Adv. Math. 44 (Cambridge University Press, 1995).CrossRefGoogle Scholar
Mörters, P. and Peres, Y.. Brownian motion. Cambridge Series in Statistical and Probabilistic Math. vol. 30 (Cambridge University Press, 2010).Google Scholar
Peres, Y. and Sousi, P.. Dimension of fractional Brownian motion with variable drift. Probab. Theory Related Fields 165, no. 3-4 (2016), 771-794.CrossRefGoogle Scholar
Pitt, L. D.. Local times for Gaussian vector fields. Indiana Univ. Math.J. 27, no. 2 (1978), 309-330.CrossRefGoogle Scholar
Revus, D. and Yor, M.. Continuous Martingales and Brownian Motion (Springer-Verlag, 1999).CrossRefGoogle Scholar
Shieh, R.. and Xiao, Y.. Images of Gaussian random fields: Salem sets and interior points. Studia Math. 176, no. 1 (2006), 37-60.CrossRefGoogle Scholar
Taylor, S. J. and Watson, N. A.. A Hausdorff measure classification of polar sets for the heat equation. Math. Proc. Camb. Phil. Soc. 97, no. 2 (1985), 325-344.CrossRefGoogle Scholar
Xiao, Y.. Hölder conditions for the local times and the Hausdorff measure of the level sets of Gaussian random fields. Probab. Theory Related Fields 109, no. 1 (1997), 129-157 CrossRefGoogle Scholar