Inclusion of sets of regular summability matrices
Published online by Cambridge University Press: 24 October 2008
Extract
1. In this paper we wish to discuss some problems which arise from a paper by Lorentz and Zeller; see (5). If {μn} is a fixed sequence monotonically increasing to infinity, and every sequence {sn} summed by both of the regular matrices A = (amn) and B = (bmn) and satisfying sn = O{μn) is summed to the same value by both matrices, the matrices are called (μn)-consistent. The two matrices are called consistent if they are (μn)-consistent for all {μn}, μn↗∞; they are b-consistent if the bounded sequences summed by both are summed to the same value by both. The matrix A is said to be (μn)-stronger than the matrix B, if every sequence {μn} that is B summable and satisfying sn = O(μn) is also A summable. The matrix A is stronger than B if every B summable sequence is A summable; A is b-stronger if every bounded B summable sequence is A summable. The symbol A -lim x denotes the value to which the sequence x = {xn} is summed by A; Am(x) is the transformation
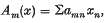
and A(x) is the sequence {Am(x)}. Let {A(i)}i ∈ I be any family, infinite or finite, of regular summability matrices. This family is called simultaneously consistent if, given any finite subset of I, say F, and any set of sequences {x(i)i ∈ F such that A(i) sums x(i) for each i in F, and such that 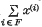 is the null sequence, then
is the null sequence, then 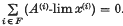 .
.
Information
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 60 , Issue 4 , October 1964 , pp. 705 - 712
- Copyright
- Copyright © Cambridge Philosophical Society 1964
References
REFERENCES
- 9
- Cited by

