Incomplete reflexive spaces without Schauder bases
Published online by Cambridge University Press: 24 October 2008
Extract
In 1968, Amemiya and Kōmura ((1), p. 275) gave an example of a separable and incomplete Montel space. Their example depended upon constructing a subspace of ω, the countable product of real lines, which had several properties and in particular had codimension 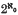 in ω. There is an error on page 276, line 5 of the proof of the Hilfssatz concerning this construction. The constructed subspace has codimension one. A more delicate construction is needed here; in fact, an example given by Webb ((7), p. 360) is sufficient to make this correction.
in ω. There is an error on page 276, line 5 of the proof of the Hilfssatz concerning this construction. The constructed subspace has codimension one. A more delicate construction is needed here; in fact, an example given by Webb ((7), p. 360) is sufficient to make this correction.
- Type
- Research Article
- Information
- Mathematical Proceedings of the Cambridge Philosophical Society , Volume 74 , Issue 1 , July 1973 , pp. 83 - 86
- Copyright
- Copyright © Cambridge Philosophical Society 1973
References
REFERENCES
- 5
- Cited by


