Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-14T07:02:27.247Z Has data issue: false hasContentIssue false
  • English
  • Français

Interior of sums of planar sets and curves

Published online by Cambridge University Press:  05 September 2018

KÁROLY SIMON  and
KRYSTAL TAYLOR
KÁROLY SIMON
Affiliation:
Budapest University of Technology and Economics, Department of Stochastics, Institute of Mathematics, and MTA-BME Stochastics Research Group, 1521 Budapest, P.O. Box 91, Hungary e-mail: simonk@math.bme.hu
KRYSTAL TAYLOR
Affiliation:
Department of Mathematics, The Ohio State, Columbus, OH, 231 W. 18th Ave., MW 706 Columbus, OH 43210 e-mail: taylor.2952@osu.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

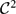Recently, considerable attention has been given to the study of the arithmetic sum of two planar sets. We focus on understanding the interior (A + Γ)°, when Γ is a piecewise ${\mathcal C}^2$ curve and A ⊂ ℝ2. To begin, we give an example of a very large (full-measure, dense, Gδ) set A such that (A + S1)° = ∅, where S1 denotes the unit circle. This suggests that merely the size of A does not guarantee that (A + S1)° ≠ ∅. If, however, we assume that A is a kind of generalised product of two reasonably large sets, then (A + Γ)° ≠ ∅ whenever Γ has non-vanishing curvature. As a byproduct of our method, we prove that the pinned distance set of C := Cγ × Cγ, γ ⩾ 1/3, pinned at any point of C has non-empty interior, where Cγ (see (1.1)) is the middle 1 − 2γ Cantor set (including the usual middle-third Cantor set, C1/3). Our proof for the middle-third Cantor set requires a separate method. We also prove that C + S1 has non-empty interior.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 168 , Issue 1 , January 2020 , pp. 119 - 148
Copyright
Copyright © Cambridge Philosophical Society 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

† This work came out of a collaboration that started at ICERM at Brown University, Rhode Island. This research was supported by the Mathematics Research Institute of the Ohio State University.

‡

Partially supported by the grant OTKA 123782, by MTA-BME Stochastics Research Group and by ICERM, by supporting his participation on one of their a semester programs in 2016.

References

REFERENCES

[1] Erdogan, B. A bilinear Fourier extension theorem and applications to the distance set problem. Int. Math. Res. Notes (2006).Google Scholar
[2] Erdős, P. and Oxtoby, J. Partitions of the plane into sets having positive measure in every non-null measurable product set. Trans. Amer. Math. Soc. 79 (1955), 91–102.Google Scholar
[3] Falconer, K. J. The geometry of fractal sets. Cambridge Tracts in Mathematics, 85 (Cambridge University Press, Cambridge, 1986).Google Scholar
[4] Hewett, D. P. and Moiola, A. On the maximal Sobolev regularity of distributions supported by subsets of Euclidean space. Anal. Appl. 15, Issue 15 (2017).Google Scholar
[5] Iosevich, A., Mourgoglou, M. and Taylor, K. On the Mattila-Sjölin theorem for distance sets. Ann. Acad. Sci. Fenn. Math. 37, no. 2 (2012).Google Scholar
[6] Iosevich, A., Taylor, K. and Uriarte-Tuero, I. Pinned geometric configurations in Euclidean space and Riemannian manifolds. https://arxiv.org/pdf/1610.00349.pdf.Google Scholar
[7] Jàrai, A. Regularity properties of functional equations in several variables. Adv. Math. 8. (Springer, New York, 2005).Google Scholar
[8] Marstrand, J. M. Packing circles in the plane. Proc. London Math. Soc. 55 (1987), 37–58.Google Scholar
[9] Mattila, P. Geometry of sets and measures in Euclidean spaces. Stud. Adv. Math. vol. 44 (Cambridge University Press, Cambridge, 1995).Google Scholar
[10] Mattila, P. Fourier analysis and Hausdrff dimension, Cambridge University Press, Studies in Advanced Mathematics vol. 150, (2015). 2, 10, 32Google Scholar
[11] Mitsis, T. On a problem related to sphere and circle packing. J. London Math Soc. (2), (1999).Google Scholar
[12] Oberlin, D. Packing Spheres and Fractal Strichartz in ℝd for d ⩾ 3. Proc. Amer. Mth. Soc. 134, no. 11 (2006).Google Scholar
[13] Rudin, W. Principles of Mathematical Analysis (International Series in Pure & Applied Mathematics) (McGraw-Hill Book co., 3rd ed., 1976).Google Scholar
[14] Palis, J. and Takens, F. Hyperbolicity and sensitive chaotic dynamics at homoclinic bifurcations. Stud. Adv. Math. vol. 35 (Cambridge University Press, 1993).Google Scholar
[15] Peres, Y. and Schlag, W. Smoothness of projections, Bernoulli convolutions, and the dimension of exceptions. Duke Math. J. 102, (2000), no. 2, 193–251.Google Scholar
[16] Piccard, S. Sur les ensembles de distances des ensembles de points d'un espace Euclidien. Memoires de l'Universite de Neuchatel, vol. 13. (L'Universite de Neuchatel, 1939). 212 pages.Google Scholar
[17] Rams, M. and Simon, K. Projections of fractal percolations. Ergodic Theory Dynam. Syst. 35, 2, (2015), 530–545.Google Scholar
[18] Shmerkin, P. On the Hausdorff dimension of pinned distance sets. Preprint (2017).Google Scholar
[19] Simon, K. and Taylor, K. Dimension and measure of sums of planar sets and curves. Preprint (2017).Google Scholar
[20] Steen, A. L. and Seebach, A. J. Counterexamples in Topology. (Springer-Verlag, Berlin, New York, 1978).Google Scholar
[21] Steinhaus, H. Sur les distances des points des ensembles de mesure positive. Fund. Math. 1, (1920), 93–104.Google Scholar
[22] Stromberg, K. An elementary proof of Steinhaus' Theorem. Proc. Amer. Math. Soc. 36, (1972), no. 1, vol. 119, no. 5 (1997), 985–1026.Google Scholar
[23] Wolff, T. Lectures on harmonic analysis. Edited by Łaba and Carol Shubin. University Lecture Series, 29 (Amer. Math. Soc., Providence, RI, 2003).Google Scholar
[24] Wolff, T. Local smoothing type estimates on Lp for large p. Geom. Funct. Anal. vol. 10 (2000).Google Scholar