Hostname: page-component-78c5997874-g7gxr Total loading time: 0 Render date: 2024-11-14T22:08:04.502Z Has data issue: false hasContentIssue false
  • English
  • Français

Isometric flows in Hilbert space

Published online by Cambridge University Press:  24 October 2008

Béla Sz.-Nagy
Béla Sz.-Nagy
Affiliation:
Szeged, Hungary
Get access Rights & Permissions [Opens in a new window]

Extract

1. Let {Vi}i≥0 be a weakly (hence also strongly) continuous semigroup of (linear) contraction operators on a Hilbert space H, i.e. |Vt| ≤ 1 ( t ≥ 0). Let Z and W denote the corresponding infinitesimal generator and cogenerator, i.e.

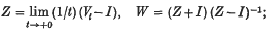
Z is in general non-bounded, but closed and densely defined, and W is a contraction operator (everywhere defined in H), such that 1 is not a proper value of W. Conversely, every contraction operator W not having the proper value 1 is the infinitesimal cogenerator of exactly one semigroup {Vi} of the above type; one has namely

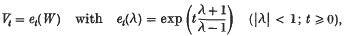
in the sense of the functional calculus for contraction operators (4).

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 60 , Issue 1 , January 1964 , pp. 45 - 49
Copyright
Copyright © Cambridge Philosophical Society 1964

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

(1)Cooper, J. L. B.One parameter semi-groups of isometric operators in Hilbert space. Ann. of Math. 48 (1947), 827–842CrossRefGoogle Scholar
(2)Halmos, P. R.Shifts on Hilbert spaces. J. Reine Angew. Math. 208 (1961), 102–112CrossRefGoogle Scholar
(3)Masani, P.Isometric flows on Hilbert spaces. Bull. American Math. Soc. 68 (1962), 624–632CrossRefGoogle Scholar
(4)Sz.-Nagy, B. and Foiaş, C.Sur les contractions de l'espace de Hilbert. III. Acta Sci. Math. Szeged, 19 (1958), 26–45Google Scholar