Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-26T17:14:14.941Z Has data issue: false hasContentIssue false
  • English
  • Français

A lower bound for Cusick’s conjecture on the digits of n + t

Part of: Elementary number theory Finite fields and commutative rings (number-theoretic aspects) Combinatorics

Published online by Cambridge University Press:  24 February 2021

LUKAS SPIEGELHOFER
LUKAS SPIEGELHOFER*
Affiliation:
Dept. Mathematics and Information Technology, Montanuniversität Leoben, Franz-Josef-Straße 18, 8700 Leoben, Austria. TU Wien, Wiedner Hauptstraße 8–10, 1040 Vienna, Austria. e-mail: lukas.spiegelhofer@unileoben.ac.at
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let S be the sum-of-digits function in base 2, which returns the number of 1s in the base-2 expansion of a nonnegative integer. For a nonnegative integer t, define the asymptotic density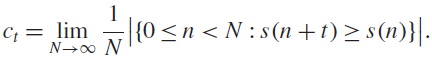

$${c_t} = \mathop {\lim }\limits_{N \to \infty } {1 \over N}|\{ 0 \le n < N:s(n + t) \ge s(n)\} |.$$
T. W. Cusick conjectured that ct > 1/2. We have the elementary bound 0 < ct < 1; however, no bound of the form 0 < α ≤ ct or ct ≤ β < 1, valid for all t, is known. In this paper, we prove that ct > 1/2 – ε as soon as t contains sufficiently many blocks of 1s in its binary expansion. In the proof, we provide estimates for the moments of an associated probability distribution; this extends the study initiated by Emme and Prikhod’ko (2017) and pursued by Emme and Hubert (2018).

MSC classification

Primary: 11A63: Radix representation; digital problems 05A20: Combinatorial inequalities
Secondary: 05A16: Asymptotic enumeration 11T71: Algebraic coding theory; cryptography
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 172 , Issue 1 , January 2022 , pp. 139 - 161
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Footnotes

†

The author acknowledges support by the project MuDeRa, which is a joint project between the FWF (Austrian Science Fund) and the ANR (Agence Nationale de la Recherche, France). Moreover, the author was supported by the FWF project F5502-N26, which is a part of the Special Research Program “Quasi Monte Carlo methods: Theory and Applications”.

References

REFERENCES

Allouche, J.-P. and Shallit, J.. The ring of k-regular sequences. Theoret. Comput. Sci. 98 (1992), 163–197.CrossRefGoogle Scholar
Bailey, R. W.. The number of weak orderings of a finite set. Soc. Choice Welf. 15 (1998), 559–562.CrossRefGoogle Scholar
Beck, J.. Probabilistic Diophantine approximation (Springer Monographs in Mathematics, Springer, Cham, 2014).CrossRefGoogle Scholar
Béjian, R. and Faure, H.. Discrépance de la suite de Van der Corput. Séminaire Delange-Pisot–Poitou. 19e année: 1977/78, Théorie des nombres, Fasc. 1, Secrétariat Math. (Paris, 1978), Exp. No. 13.Google Scholar
Bésineau, J.. Indépendance statistique d’ensembles liés à la fonction “somme des chiffres”. Acta Arith. 20 (1972), 401–416.CrossRefGoogle Scholar
Cusick, T. W., Li, Y., and Stănică, P.. On a combinatorial conjecture. Integers 11 (2011).CrossRefGoogle Scholar
Deng, G. and Yuan, P.. On a combinatorial conjecture of Tu and Deng. Integers 12 (2012).Google Scholar
Drmota, M., Kauers, M., and Spiegelhofer, L.. On a conjecture of Cusick concerning the sum of digits of n and n + t. SIAM J. Discrete Math. 30 (2016), 621–649.CrossRefGoogle Scholar
Drmota, M., Larcher, G., and Pillichshammer, F.. Precise distribution properties of the van der Corput sequence and related sequences. Manuscripta Math. 118 (2005), 11–41.CrossRefGoogle Scholar
Emme, J. and Hubert, P.. Central limit theorem for probability measures defined by sum-of-digits function in Base 2. Ann. Sc. Norm. Super. Pisa Cl. Sci. (5) 19 (2019), 757–780.Google Scholar
Emme, J. and Hubert, P.. Normal distribution of correlation measures of binary sum-of-digits functions. Preprint (2018), http://arxiv.org/abs/1810.11234.Google Scholar
Emme, J. and Prikhod’ko, A.. On the asymptotic behavior of density of sets defined by sum-of-digits function in base 2. Integers 17 (2017).Google Scholar
Flajolet, P. and Sedgewick, R.. Analytic Combinatorics. (Cambridge University Press, Cambridge, 2009).CrossRefGoogle Scholar
Flori, J.-P.. Fonctions booléennes, courbes algébriques et multiplication complexe. Doctoral thesis, Télécom ParisTech (2012).Google Scholar
Flori, J.-P., Randriambololona, H., Cohen, G. and Mesnager, S.. On a conjecture about binary strings distribution. In Sequences and Their Applications - SETA 2010 Springer Berlin/Heidelberg (Ed.), (2010), 346–358.CrossRefGoogle Scholar
Morgenbesser, J. F. and Spiegelhofer, L.. A reverse order property of correlation measures of the sum-of-digits function. Integers 12 (2012).Google Scholar
Pronov, P. D. and Atanassov, E. Y.. On the distribution of the van der Corput generalised sequences. C. R. Acad. Sci. Paris Sér. I Math. 307 (1988), 895–900.Google Scholar
Robbins, H.. A remark on Stirling’s formula. Amer. Math. Monthly 62 (1955), 26–29.Google Scholar
Spiegelhofer, L.. Discrepancy results for the van der Corput sequence. Unif. Distrib. Theory 13 (2018), 57–69.CrossRefGoogle Scholar
Spiegelhofer, L.. Approaching Cusick’s conjecture on the sum-of-digits function. Integers 19 (2019).Google Scholar
Spiegelhofer, L. and Wallner, M.. The Tu–Deng conjecture holds almost surely. Electron. J. Combin. 26 (2019)CrossRefGoogle Scholar
Tu, Z. and Deng, Y.. A conjecture about binary strings and its applications on constructing Boolean functions with optimal algebraic immunity. Des. Codes Cryptogr. 60 (2011), 1–14.CrossRefGoogle Scholar
Tu, Z. and Deng, Y.. Boolean functions optimizing most of the cryptographic criteria. Discrete Appl. Math. 160 (2012), 427–435.CrossRefGoogle Scholar