Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T06:21:49.397Z Has data issue: false hasContentIssue false
  • English
  • Français

Maximal prime homomorphic images of mod-p Iwasawa algebras

Part of: Modules, bimodules and ideals Rings and algebras arising under various constructions

Published online by Cambridge University Press:  05 March 2021

WILLIAM WOODS
WILLIAM WOODS*
Affiliation:
Pathways Department, University of Essex, Colchester, CO4 3SQ, e-mail: billywoods@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

Let k be a finite field of characteristic p, and G a compact p-adic analytic group. Write kG for the completed group ring of G over k. In this paper, we describe the structure of the ring kG/P, where P is a minimal prime ideal of kG. We give an explicit isomorphism between kG/P and a matrix ring with coefficients in the ring 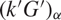${(k'G')_\alpha }$ , where 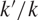$k'/k$ is a finite field extension, 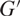$G'$ is a large subquotient of G with no finite normal subgroups, and (–)α is a “twisting” operation that preserves many desirable properties of the ring structure. We demonstrate the usefulness of this isomorphism by studying the correspondence induced between certain ideals of kG and those of 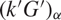${(k'G')_\alpha }$ , and showing that this preserves many useful “group-theoretic” properties of ideals, in particular almost-faithfulness and control by a closed normal subgroup.

MSC classification

Primary: 16S34: Group rings , Laurent polynomial rings 16S35: Twisted and skew group rings, crossed products 16D25: Ideals
Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 171 , Issue 2 , September 2021 , pp. 387 - 419
Copyright
© The Author(s), 2021. Published by Cambridge University Press on behalf of Cambridge Philosophical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aljadeff, E. and Robinson, D.J.S.. Semisimple algebras, Galois actions and group cohomology. J. Pure Appl. Alg., 94, (1994), 1–15.CrossRefGoogle Scholar
Ardakov, K.. Localisation at augmentation ideals in Iwasawa algebras. Glas. Math. J., 48(2), (2006), 251–267.CrossRefGoogle Scholar
Ardakov, K.. The controller subgroup of one-sided ideals in completed group rings. Contemp. Math., 562, (2012), 11–26.CrossRefGoogle Scholar
Ardakov, K.. Prime ideals in nilpotent Iwasawa algebras. Invent. math., 190(2), (2012), 439–503.CrossRefGoogle Scholar
Ardakov, K. and Brown, K.A.. Primeness, semiprimeness and localisation in Iwasawa algebras. Trans. Amer. Math. Soc., 359, (2007), 1499–1515.CrossRefGoogle Scholar
Ardakov, K. and Wadsley, S.J.. Characteristic elements for p-torsion Iwasawa modules. J. Algebraic Geom., 15, (2006), 339–377.CrossRefGoogle Scholar
Brumer, A.. Pseudocompact algebras, profinite groups and class formations. J. Algebra., 4, (1966), 442–470.CrossRefGoogle Scholar
Dixon, J.D., du Sautoy, M.P.F., Mann, A., and Segal, D.. Analytic Pro-p Groups., (Cambridge University Press, 1999).CrossRefGoogle Scholar
Mac Lane, S.. Homology., (Springer, 1963).CrossRefGoogle Scholar
McConnell, J.C. and Robson, J.C.. Noncommutative Noetherian Rings., (American Mathematical Society, 2001).CrossRefGoogle Scholar
Passman, D. S.. Algebraic Structure of Group Rings., (John Wiley & Sons, 1977).Google Scholar
Passman, D. S.. Infinite Crossed Products., (Academic Press Inc., 1989).Google Scholar
Roseblade, J.E.. Prime ideals in group rings of polycyclic groups. Proc. London Math. Soc., 36, (1978), 385–447.CrossRefGoogle Scholar
The Stacks Project Authors. Stacks Project. http://stacks.math.columbia.edu, (2016).Google Scholar
Warner, S.. Topological Rings. 178 (North-Holland Mathematics Studies, 1993).Google Scholar
Woods, W.. On the structure of virtually nilpotent compact p-adic analytic groups. J. Group Theory 21(1), (2018), 165–188.CrossRefGoogle Scholar