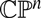Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Oganesyan, Vardan
2023.
Zoo of monotone Lagrangians in $${\mathbb {C}}P^n$$.
Selecta Mathematica,
Vol. 29,
Issue. 5,