Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-15T01:21:06.456Z Has data issue: false hasContentIssue false
  • English
  • Français

A note on homology surgery and the Casson–Gordon invariant

Published online by Cambridge University Press:  24 October 2008

Selman Akbulut
Selman Akbulut
Affiliation:
Rutgers University, New Jersey 08903, U.S.A.
Get access Rights & Permissions [Opens in a new window]

Extract

We give a ‘picture’ proof to a theorem of M. Freedman (2) which shows the failure of the 4-dimensional homology surgery theory and the homology splitting theorem. Our proof employs the language of the framed links (3) and it involves calculating Casson-Gordon invariant of a certain algebraically slice knot. We use framed links to represent 1-connected 4-manifolds with boundary by attaching 2-handles along them onto B4 via the framings. We adapt the notation ≈ for diffeomorphisms, and 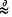for diffeomorphisms between the boundaries of manifolds. Here manifolds refer to smooth manifolds.

Type
Research Article
Information
Mathematical Proceedings of the Cambridge Philosophical Society , Volume 85 , Issue 2 , March 1979 , pp. 335 - 344
Copyright
Copyright © Cambridge Philosophical Society 1979

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

(1)Casson, A. J. and Gordon, C. McA. Cobordism of classical knots. I.H.E.S. Notes.Google Scholar
(2)Freedman, M. H. Knot theory and 4-dimensional surgery.Google Scholar
(3)Kirby, R. C. A calculus for framed links in S 3.Google Scholar