Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Oort, F.
1963.
Natural maps of extension functors.
Indagationes Mathematicae (Proceedings),
Vol. 66,
Issue. ,
p.
559.


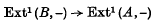
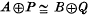 . One can ask whether these theorems remain true for higher extension functors.
. One can ask whether these theorems remain true for higher extension functors.