Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Yoshino, Takashi
1965.
On the spectrum of a hyponormal operator.
Tohoku Mathematical Journal,
Vol. 17,
Issue. 3,
Whitley, Robert
1968.
The Spectral Theorem for a Normal Operator.
The American Mathematical Monthly,
Vol. 75,
Issue. 8,
p.
856.
Berberian, S. K.
1970.
Some conditions on an operator implying normality.
Mathematische Annalen,
Vol. 184,
Issue. 3,
p.
188.
Goldberg, Moshe
1979.
On certain finite dimensional numerical ranges and numerical radii†.
Linear and Multilinear Algebra,
Vol. 7,
Issue. 4,
p.
329.
Harte, Robin
and
Searc�id, M�che�l �
1986.
Positive elements and theB * condition.
Mathematische Zeitschrift,
Vol. 193,
Issue. 1,
p.
1.
Komornik, Vilmos
2016.
Lectures on Functional Analysis and the Lebesgue Integral.
p.
151.
Komornik, Vilmos
2016.
Lectures on Functional Analysis and the Lebesgue Integral.
p.
197.
Komornik, Vilmos
2016.
Lectures on Functional Analysis and the Lebesgue Integral.
p.
211.
Komornik, Vilmos
2016.
Lectures on Functional Analysis and the Lebesgue Integral.
p.
305.
Komornik, Vilmos
2016.
Lectures on Functional Analysis and the Lebesgue Integral.
p.
257.
Komornik, Vilmos
2016.
Lectures on Functional Analysis and the Lebesgue Integral.
p.
3.
Komornik, Vilmos
2016.
Lectures on Functional Analysis and the Lebesgue Integral.
p.
55.
Komornik, Vilmos
2016.
Lectures on Functional Analysis and the Lebesgue Integral.
p.
169.
Komornik, Vilmos
2016.
Lectures on Functional Analysis and the Lebesgue Integral.
p.
341.
Komornik, Vilmos
2016.
Lectures on Functional Analysis and the Lebesgue Integral.
p.
119.
Garcia, Stephan Ramon
Mashreghi, Javad
and
Ross, William T.
2018.
Finite Blaschke Products and Their Connections.
p.
209.
Baklouti, Hamadi
and
Feki, Kais
2020.
Commuting Tuples of Normal Operators in Hilbert Spaces.
Complex Analysis and Operator Theory,
Vol. 14,
Issue. 6,
M., Salim Dawood
and
Eidi, Jaafer Hmood
2021.
On (P*-N) quasi normal operators Of order "n" In Hilbert space.
Al-Mustansiriyah Journal of Science,
Vol. 32,
Issue. 1,
p.
10.
Mortad, Mohammed Hichem
2022.
Counterexamples in Operator Theory.
p.
169.
Dietz, Zach
Lippitt, William
and
Sethuraman, Sunder
2023.
Stick-Breaking processes, Clumping, and Markov Chain Occupation Laws.
Sankhya A,
Vol. 85,
Issue. 1,
p.
129.


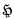 is said to be
is said to be 